This post is also available in the following languages. Japanese, English

암호 알고리즘 AES-GCM-SIV 최적화 작업 소개

한주홍2022-11-17

Security R&D 팀에서 보안 기술 연구 및 보안 컨설팅을 담당하고 있습니다.

들어가며

안녕하세요. Security R&D 팀에서 보안 기술 연구 및 보안 컨설팅을 담당하고 있는 한주홍입니다. 세상에는 다양한 보안 기술이 있습니다. 그중에서 암호 알고리즘은 데이터 보안을 위해서 꼭 필요한 기술입니다. LINE에서도 중요한 데이터를 보호하기 위해 여러 암호 알고리즘을 적용해 서비스를 제공하고 있으며, 저희 팀에서는 보안을 잘 모르는 다른 LINE 개발자분들도 쉽고 편하게 사용할 수 있도록 여러 암호 알고리즘을 라이브러리로 만들어 제공하고 있습니다.

AES-GCM-SIV도 그중 하나입니다. 최근에는 Tink와 BoringSSL 등 여러 라이브러리에서 AES-GCM-SIV를 제공하고 있지만, 저희 팀에서 처음 도입할 때에는 이런 라이브러리가 없었기 때문에 직접 구현해야 했습니다. 이에 당시 저희 팀원분들께서 C 언어로 코드를 작성해서 이를 JAVA와 Android, Go와 같은 다양한 환경으로 포팅해 다른 팀에서 편하게 사용할 수 있도록 제공했고, 현재 LINE 클라이언트(Android 및 iOS)와 LINE 메시지 스티커 암호화 등 여러 서버 사이드 프로젝트에서 사용하고 있습니다.

이렇게 점점 많은 팀에서 사용하게 되면서 저희 팀에서는 많은 분들이 이용하는 ARM 환경에서의 최적화 작업도 필요하다고 판단했는데요. 이번 글에서는 최근 마무리한 ARM 환경 최적화 작업 과정과 그 결과를 공유하려고 합니다. 글은 다음과 같은 순서로 진행합니다.

AES-GCM-SIV 소개
- 알고리즘 구조
- 장점과 단점
최적화 과정 소개
- 최적화 작업
- 최적화 결과 비교
그 외 개선 사항 및 장점
- 유지 보수 및 가독성을 위해 내장 함수로 교체
- AES 명령어를 이용한 구현으로 부채널 공격 내성까지 확보
마치며
- 참고 문헌

AES-GCM-SIV 소개

정보 보안에 관심이 있으시다면 AES-GCM이 가장 인기 있는 인증 암호 알고리즘 중 하나라는 것을 아시겠지만, AES-GCM-SIV[1]는 조금 생소할 수도 있습니다. 기존 GCM 운영 모드의 보안을 조금 더 개선한 알고리즘이라고 생각하시면 됩니다. 기존 GCM 알고리즘은 서로 다른 두 개의 데이터를 암호화할 때 동일한 키와 논스(nonce) 쌍을 재사용하는 경우 취약점이 발생했습니다[2]. 물론 그렇기 때문에 동일한 키와 논스 쌍을 재사용하지 않아야 한다고 권고하고 있지만[3], 그 사실을 모르는 사용자는 의도치 않게 취약점을 만들어 낼 수 있습니다. AES-GCM-SIV는 이 문제에 내성을 갖도록 설계한 알고리즘입니다. AES-GCM-SIV이 생소하신 분들을 위해 구조와 장단점을 조금 더 알아보겠습니다.

알고리즘 구조

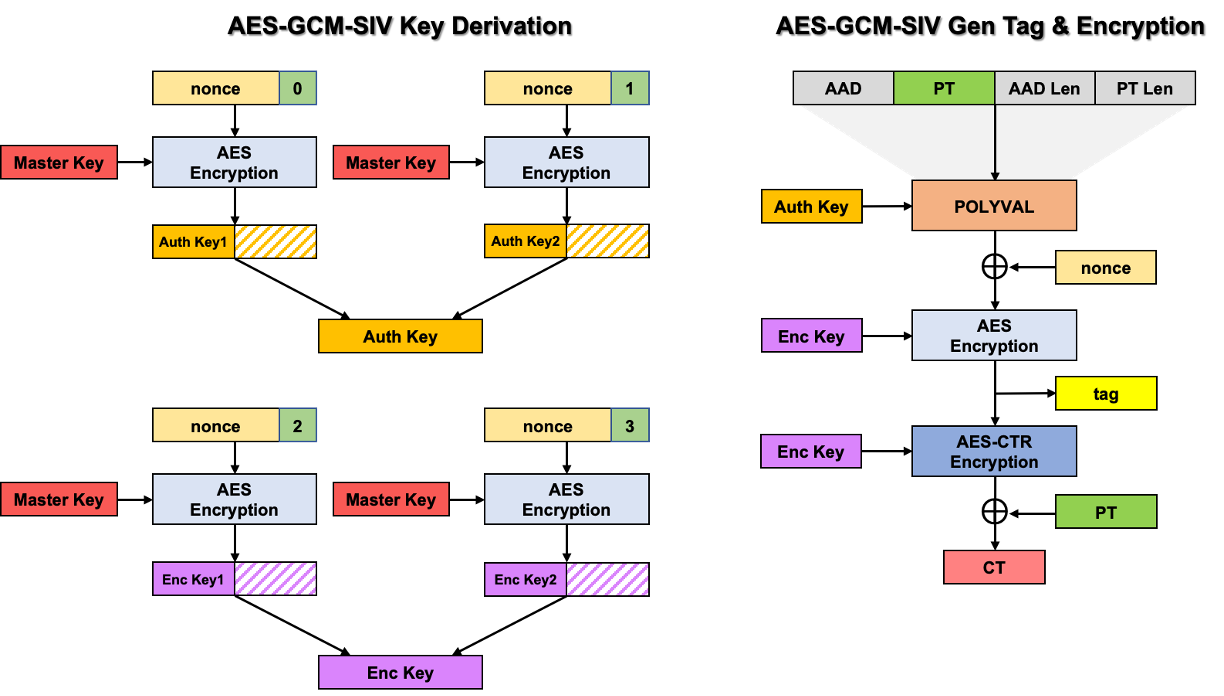
AES-GCM-SIV는 크게 키 유도와 메시지 인증, 메시지 암호화, 이렇게 세 부분으로 구분할 수 있습니다. 알고리즘 작동 초기 단계에서는 키 유도 함수에서 마스터 키를 입력으로 받아 메시지 인증 키와 암호화 키를 생성합니다. 이후 POLYVAL과 AES 알고리즘을 거쳐 메시지 인증에 사용하는 태그를 생성하고, 이 값을 카운터 값으로 사용해 암호화하는 과정으로 마무리됩니다. 초기에 인증 키와 암호화 키를 별도로 생성한다는 점과 인증값을 먼저 계산하고 이를 카운터로 사용해 암호문에 바인딩시킨다는 점 때문에 이전 GCM 운영 모드 보다 더욱 안전해졌습니다.

장점과 단점

AES-GCM-SIV 역시 여느 암호 알고리즘처럼 장단점이 있습니다.

장점

첫 번째 장점은 안전성이 뛰어나다는 것입니다. AES-GCM-SIV의 주요 콘셉트는 앞서 언급한 것처럼 메시지를 암/복호화할 때 마스터 키를 이용해 암호화 키와 인증 키를 따로 생성한다는 것입니다. 암호화 키와 인증 키는 AES-CTR 모드에서 출력된 난수처럼 보이는 충분히 긴 키 스트림으로 생성되며, 이와 같이 난수처럼 보이는 긴 키 스트림은 공격자가 예측하기 어렵습니다.

또한 공격자에게 암호화 키나 인증 키가 노출되더다라도 다른 키와 마스터 키에는 영향이 가지 않습니다. 그저 새로운 논스로 인증 키와 암호화 키 쌍을 다시 유도하면 됩니다. 일반적으로 다른 알고리즘은 키 유도 과정 없이 마스터키를 직접 사용하는 경우가 많은데요. 물론 다른 알고리즘으로도 프로토콜을 잘 설계한다면 비슷한 구조로 만들 수 있겠지만, AES-GCM-SIV은 설계부터 이런 요소를 내재화했기 때문에 보안 프로토콜 설계에 익숙하지 않은 분들도 실수를 최소화할 수 있다는 것이 큰 장점입니다.

안전성과 관련해 또 다른 장점은 기존 인증 암호 알고리즘에서 발생했던 논스 재사용 문제에 내성이 있다는 것입니다. 기존 GCM 알고리즘에서는 공격자가 같은 키와 논스로 만든 암호문 한 쌍을 가진 상태에서 둘 중 하나의 평문을 알 수 있다면 나머지 평문 역시 복구할 수 있습니다. 이런 상황에서는 인증키 역시 쉽게 복구할 수 있기 때문에 공격자는 필요한 평문과 암호문, 인증값 쌍들을 원하는 만큼 만들어 낼 수 있습니다. 반면 AES-GCM-SIV에서는 같은 상황에서 공격자가 두 데이터를 같은 데이터로 암호화했는지만 알 수 있을 뿐 다른 어떤 정보도 얻지 못합니다(물론 이 정보 역시 공격자가 알 수 없으면 좋겠지만 이는 결정론적 알고리즘에서는 어쩔 수 없는 한계입니다).

두 번째 장점은 알고리즘을 구현할 때 다양한 하드웨어 자원을 이용할 수 있다는 것입니다. AES-GCM-SIV는 위 그림에서 알 수 있듯이 내부에서 암/복호화 및 인증키 생성에 AES 알고리즘을 사용합니다. AES 알고리즘은 꽤 오래전부터 전 세계적으로 널리 사용됐기 때문에 현재 소프트웨어보다 성능이 월등한 하드웨어 가속기를 탑재한 CPU들이 많이 있습니다. 이는 구현할 때 많은 이점이 됩니다. 또한 인증 태그를 생성하기 위한 POLYVAL 함수는 이진 유한체 위에서의 연산이 필요한데 최근 많은 CPU들이 이를 위한 별도 명령 집합(carry-less multiplication)을 제공하고 있습니다. 따라서 AES-GCM-SIV는 가장 많은 연산량이 필요한 데이터 인증 과정과 암/복호화 과정에서 다양한 하드웨어 자원을 사용할 수 있으며, 이는 소프트웨어 구현만 가능한 다른 알고리즘과 비교해 정말 큰 이점입니다. 게다가 POLYVAL 함수는 GCM 운영 모드에서 사용하는 수식과 유사하지만 리틀 엔디안(little-endian) 아키텍처에서 더욱 효율적으로 계산할 수 있도록 변형된 수식을 사용하기 때문에 GCM 내부의 GHASH 구현체를 POLYVAL 알고리즘 구현에 재사용할 수 있는 장점도 있습니다.

단점

이제 단점을 살펴보겠습니다. 이미 눈치채신 분도 계시겠지만 장점으로 언급했던 안전한 구조 때문에 소프트웨어로 구현하면 다른 알고리즘에 비해 성능이 조금 떨어집니다. 암/복호화할 때마다 내부에서 인증 키와 암호화 키 생성을 매번 수행하기 때문에 한 번 생성된 라운드 키를 저장하고 여러 번 재사용하는 다른 알고리즘에 비해 성능이 떨어질 수밖에 없습니다.

또 다른 단점은 알고리즘 구조 때문에 암/복호화 전체 과정에서 데이터를 스트림 형태로 처리하지 못한다는 것입니다. 이는 암/복호화 과정을 진행하기 전에 부가 인증 데이터(AAD)와 평문/암호문에 대한 인증 과정을 선행해야 하기 때문입니다. 스트림 형태로 데이터를 처리할 수 없기 때문에 암/복호화 과정을 진행하기 전에 모든 데이터와 메모리 자원을 사용할 수 있어야 합니다.

하지만, 이런 단점들은 성능과 관련된 단점이기 때문에 하드웨어 가속기와 특정 명령 집합을 사용해 구현한다면 대부분 보완할 수 있고, 결과적으로 사용자가 체감하기 어려운 차이로 만들 수 있습니다.

최적화 과정 소개

앞서 언급했다시피 AES-GCM-SIV 알고리즘을 구현할 때에는 AES 하드웨어 가속기와 GCM 운영 모드를 위한 특별한 명령 집합을 사용할 수 있습니다. 기존에 저희 팀에서 제공하는 라이브러리는, Intel x86-64 버전에는 Mbed TLS의 AES 코드를 사용해 이와 같은 최적화 요소를 추가해 놓았지만 ARM 아키텍처 버전에는 소프트웨어 환경만을 고려한 구현체만 있었습니다. 그런데 다른 팀에서 사용하는 빈도가 조금씩 늘어갔고 최근 저희가 사용하는 대다수 장비가 ARM 아키텍처 환경이라는 사실을 고려했을 때 ARM 환경에서의 최적화 역시 필요하다고 판단했습니다. 최적화는 암호 하드웨어 가속 기능을 지원하는 Armv8-A CPU들에만 적용할 수 있지만, 최신 ARM CPU는 이 기능을 지원하는 경우가 많다는 사실도 고려했습니다.

x86-64 환경에서 구현하는 것과 ARM 환경에서 구현하는 것은 기본적으로 명령 집합만 조금 다를 뿐 거의 비슷하기 때문에 이번 글에서는 ARM 환경에서 구현하는 것만 살펴보겠습니다.

최적화 작업

일반적인 최적화 과정은 소스 코드 작성 후 프로파일링 도구를 이용해 최적화가 필요한 위치를 찾아서 해당 부분을 집중적으로 최적화하는 방식으로 진행합니다. 하지만 이번에는 최적화할 대상이 AES-GCM-SIV 알고리즘 내부에서 사용하는 암호화 과정과 데이터 인증 과정으로 이미 정해져 있기 때문에 따로 프로파일링하지 않고 해당 부분에 초점을 맞춰 최적화 작업을 시작했습니다.

최적화와 관련해서, 보통 상황에 맞는 자료형과 문법, 알고리즘으로 프로그래밍한 뒤 여기서 몇 가지 테크닉을 사용하면 컴파일러가 더 멋지게 최적화해 주는 경우가 많습니다. 하지만 암호 알고리즘을 최적화할 때는 컴파일러 최적화로는 부족한 부분이 몇 군데 있습니다. 암호 연산 과정에는 다양한 수학 연산에서 발생하는 캐리 처리부터 벡터 연산 최적화, CPU 아키텍처별 파이프라이닝 구성, 데이터 로드(load)와 저장(store)을 위한 레지스터 제어까지 최적화할 요소가 많은데요. 컴파일러가 이런 부분을 다 최적화해 주지는 못합니다. 따라서 많은 암호 엔지니어가 이 부분까지 최적화하기 위해 어셈블리어를 사용합니다. 어셈블리어는 프로그래밍하기가 훨씬 까다롭고 개발 시간도 더 오래 걸리지만 하드웨어 자원을 최대한 효율적으로 사용할 수 있다는 장점이 있습니다. 저희 역시 어셈블리어를 사용해 개발했는데요. 어떻게 최적화했는지 살펴보겠습니다.

AES 구조 및 관련 명령어 소개

앞서 살펴본 것처럼 AES-GCM-SIV를 최적화하기 위해서는 내부에서 사용하는 AES 알고리즘을 최적화할 필요가 있습니다. 하드웨어 가속기를 사용했지만 설명할 최적화 내용이 AES 구조와도 관계가 있기 때문에 간단히 설명하고 넘어가겠습니다(각 과정별 세부 내용은 FIPS-197[4] 문서에 자세히 나와 있으니 이 문서를 참조해 주세요).

AES는 키 확장 부분과 암/복호화 부분으로 구분할 수 있습니다. 키 확장 부분은 암호화 과정의 각 라운드 마지막 단계에서 사용하는 라운드 키를 생성하는 단계입니다. 하나의 라운드 키는 32-bit 크기 워드 네 개로 생성됩니다. 암호화 과정은 아래 그림처럼 구성되는데요. 마지막 라운드에서 MixColumns 연산이 빠진 것과, 암호 키 크기가 128/192/256 bit 크기로 나뉘지만 생성되는 라운드 키는 모두 블록 크기에 맞는 128-bit라는 점이 중요합니다.

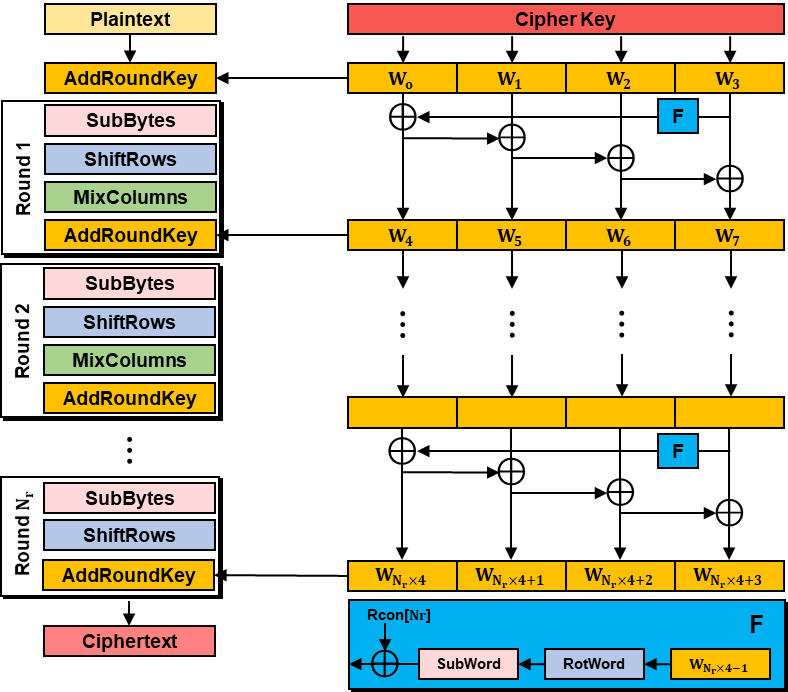
이제 ARM 아키텍처에서 사용할 AES 관련 명령어를 알아보겠습니다. 앞서 언급한 것처럼 AES-GCM-SIV는 내부에서 CTR 운영 모드를 사용하기 때문에 AES 복호화 함수를 사용하지 않습니다. 따라서 사용할 명령어는 단 두 개입니다[5][6].

AESE - AES single round encryption

AddRoundKey, SubBytes, ShiftRows 연산이 모두 아래와 같이 처리됩니다.

AESE <Vd>.16B, <Vn>.16B
{
	bits(128) operand1 = v[d];
	bits(128) operand2 = v[n];
	bits(128) result;

	result = operand1 EOR operand2;
	result = AESSubBytes(AESShiftRows(result));

	v[d] = result;
}

AESMC - AES MixColumns
- 나머지 MixColumns 연산을 처리합니다.

키 확장 과정

키 확장 과정은 전체 작동 시간에서 많은 부분을 차지하지는 않았습니다. 다만 AES-GCM-SIV에서는 매 암호화마다 키 확장 과정을 여러 번 수행하기 때문에 장기적인 사용 관점에서 조금이라도 개선의 여지가 있다면 최적화하는 것이 좋다고 판단했습니다.

일반적으로 암호 알고리즘 최적화에는 많은 연산이 필요한 부분들을 미리 계산해 테이블로 만들어 두는 룩업(lookup) 테이블 방식을 주로 사용합니다. 메모리를 추가로 소비하는 대신 해당 연산 과정을 단순 테이블 참조로 대체할 수 있기 때문입니다. AES 소프트웨어로 구현할 때도 연산량을 최소화하기 위해 이 방식을 사용합니다. 보통 AES를 구현한 오픈소스를 보면 S-Box로 명명된 배열이 할당된 것을 볼 수 있습니다. 이 S-Box(substitution table)가 암호화 과정에서의 SubBytes 변환에 대응되는 테이블이며, 키 확장 과정의 SubWord와 암호화 과정의 SubBytes에서 사용됩니다.

앞서 살펴본 AES 구조 그림에서 알 수 있듯이, 키 확장 과정에는 이전 라운드 키의 마지막 워드에 RotWord와 SubWord 연산을 적용하는 과정이 있습니다. 이때 RotWord와 SubWord 연산은 기본적으로 암호화 부분의 ShiftRows와 SubBytes와 같고, 한 워드에 대해서만 적용한다는 점만 다릅니다. 따라서 비록 키 확장 과정만을 위한 특별한 명령어는 없지만 암호화 과정에서 사용하는 명령어를 이용해 아래와 같이 최적화할 수 있습니다.

	LDR W0, ="#RCON"
	MOV W15, W12
	DUP v1.4s, W15
	EOR.16b v0, v0, v0
	AESE v0.16b, v1.16b
	UMOV W15, v0.s[0]
	ROR W15, W15, #8
	EOR W9, W9, W15
	EOR W9, W9, W0
	EOR W10, W10, W9
	STP W9, W10, [%[rk]], #8
	EOR W11, W11, W10
	EOR W12, W12, W11
	STP W11, W12, [%[rk]], #8

위 코드 W15에는 이전 라운드 키의 마지막 워드 값이 저장된 상태입니다. 이를 DUP 명령어를 사용해 v1 벡터 레지스터의 각 워드 위치로 복사하고, 이후 AESE 명령어로 산출된 결괏값을 가져와 적절한 비트 연산으로 마무리합니다. 여기서 중요한 구현 포인트는 AESE 이전에 호출된 EOR 명령어에 있습니다. EOR 명령어는 입력 레지스터가 서로 같으면 같은 값을 XOR하는 의미가 돼 연산 결괏값은 반드시 0이 됩니다. 즉, 값을 0으로 초기화해 AddRoundKey 과정을 없애는 역할을 합니다. EOR 명령어를 사용한 변수 초기화는 어셈블리어 프로그래밍에서 많이 사용하는 방법이니 기억해 놓으면 다른 코드를 볼 때 도움이 되실 거라고 생각합니다.

앞선 AESE 연산 과정에 Vd 값을 0으로 만들고 정리하면 다음과 같습니다.

AESE Vd, Vn 
{
	operand1 = Vd;
	operand2 = Vn;
	result;

	operand2 = operand1 EOR operand2; // operand2 = 0 EOR operand2;
	result = AESSubBytes(AESShiftRows(operand2));

	vd = result;
}

AESE 명령어 시작 부분에 operand1과 operand2를 XOR하는 부분이 있기 때문에 Vd에 0이 입력되지 않는다면 이후 ShiftRows와 SubBytes 연산의 입력값은 operand2가 아닌 다른 값이 될 겁니다.

암호화 과정

암호화 과정에서도 키 확장 과정과 같이 룩업 테이블 방식을 사용해 구현하는 경우가 많습니다. 암호화 과정 테이블에는 SubBytes, ShiftRows, MixColumns 연산 결괏값이 사전에 계산돼 있어서, 암호화 과정은 테이블 참조와 몇 번의 비트 연산 후 라운드 키와 XOR하는 과정으로 마무리됩니다. 그런데 이때 하드웨어 가속 명령어를 사용하면 프로세서마다 차이는 있지만 대략 6 사이클 내로 단일 라운드 암호화가 끝나며 테이블 참조를 할 필요가 없어집니다. 실제 구현 내용이 궁금하신 분들이 계실 것 같아서 128-bit 키 암호화만 작성해 봤습니다.

	// Load plaintext
	LD1.16b {v0}, [%[in]]
	
	// Load roundkeys
	LD1.16b {v1-v4}, [%[rk]], #64

	// 1 to 4 round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v3.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v4.16b
	AESMC v0.16b, v0.16b

	// Load roundkeys
	LD1.16b {v1-v4}, [%[rk]], #64

	// 5 to 8 round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v3.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v4.16b
	AESMC v0.16b, v0.16b
	
	// Load roundkeys
	LD1.16b {v1-v3}, [%[rk]]

	// 9 to last round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b

	// Last AddRoundKey
	EOR.16b v0, v0, v3

	// Store ciphertext
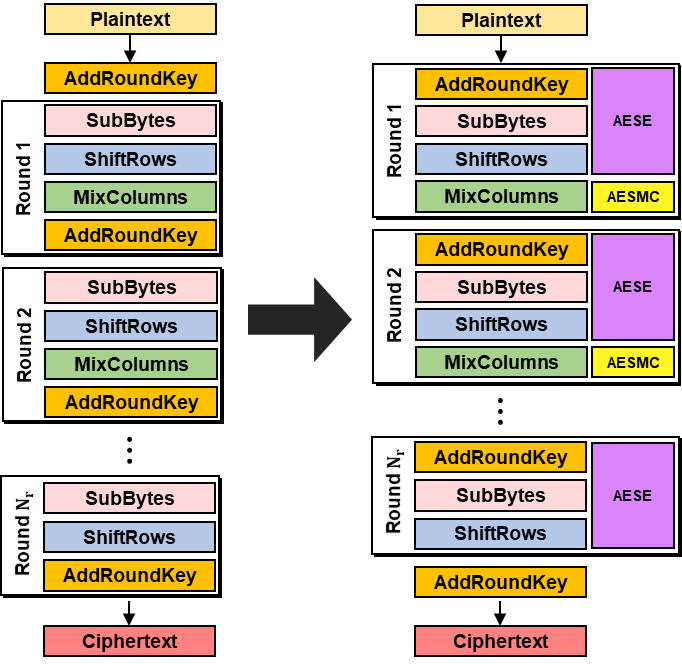
	ST1.16b {v0}, [%[out]]

코드를 보면 v0 레지스터에는 평문을, v1~v4까지는 4개 라운드 키를 한 번에 로드해 각 라운드 암호화마다 사용하는 것을 알 수 있습니다(물론 이는 하나의 예시일 뿐이고, 라운드 키 로드 개수와 사용하는 벡터 레지스터 개수 등은 설계에 따라 다를 수 있습니다). 그런데 위 코드에서 조금 이상한 점을 느끼셨나요? 잘 생각해 보면 앞서 제가 말씀드렸던 구조와 잘 매치되지 않습니다. AES 표준 문서에서는 각 라운드를 SubBytes, ShiftRows, MixColumns, AddRoundKey 순서로 구성했습니다. 그리고 마지막 라운드에서 MixColumns 과정이 빠집니다. 하지만, AESE 명령어의 내부 작동 과정을 생각해 보면 잘 맞지 않습니다. 이때 아래 그림과 같이 생각해야 과정이 자연스럽게 전개됩니다. 마지막 라운드에서는 AESE 명령어만 호출하고 AddRoundKey 과정을 거치면 되는데 이때 AddRoundKey는 위 코드와 같이 XOR로 간단히 처리됩니다.

태그 생성 과정

이제 태그 생성 과정 최적화에 대해 말씀드리겠습니다. AES-GCM-SIV 알고리즘은 GCM 운영 모드와 마찬가지로 Galois 모드 기반 인증 메커니즘을 사용합니다. 여기서는 POLYVAL로 부르는데요. 이는 단지 GCM 모드의 GHASH에서 사용하는 기약 다항식의 계수가 반대로 표현된 것입니다[1]. 따라서 리틀 엔디안 환경에서는 더 효율적으로 계산할 수 있습니다. 아래 식은 이진 유한체 위에 정의된 수식이기 때문에 POLYVAL 연산을 하기 위해서는 이진 유한체 위에서 덧셈, 뺄셈, 곱셈, 역원 연산을 해야 합니다.

$\begin{align*} \textbf{Polynomial of AES-GCM-SIV} &\boldsymbol{:x^{128}\boldsymbol{+}x^{127}+x^{126}+x^{121}+1}\\\textbf{Polynomial of GCM} &\boldsymbol{:x^{128}+x^7+x^2+x+1}\end{align*}$

이진 유한체 위에서의 표현 방식과 연산이 생소하신 분들을 위해 간단히 설명하고 넘어가겠습니다. 먼저, 이진 다항식은 각 항의 계수가 0 또는 1로 구성됩니다. 이는 컴퓨터가 각 비트를 0 또는 1로 표현하는 것과 같이 생각할 수 있습니다. 간단히 예를 들어 보면, $x^7+x^2+x+1$ 은 $10000111_{(2)}$ 로 표현할 수 있습니다.

이렇게 표현하면 차수가 높아져도 배열 안에 모든 항을 표현할 수 있습니다. 또한, 이진 유한체 위에서의 연산은 캐리가 전파되지 않는다는 재미있는 성질이 있습니다. 그래서 덧셈, 뺄셈 연산은 각 피연산자끼리의 XOR로 처리되고, 곱셈 연산은 일반적인 곱셈과 비슷하지만 곱셈 과정에서의 덧셈 연산이 캐리 전파 없이 XOR로 처리됩니다.

이제, 본격적으로 POLYVAL 함수 정의와 최적화 방법에 대해 말씀드리겠습니다. POLYVAL 함수의 정의는 다음과 같습니다[1].

$\\\boldsymbol{Polyval(H,X_1,X_2,\dots,X_s)=S_s}\textbf{,}\\\textbf{where }\boldsymbol{S_j = }\begin{cases}\boldsymbol{0}&\textbf{if }\boldsymbol{j = 0}\\\boldsymbol{dot(S_{j-1}+X_j,H)}&\textbf{if }\boldsymbol{1\le j\le s} \textbf{,}\\\end{cases}\\\textbf{and }\boldsymbol{dot(a,b)=a \times b \times X^{-128}}$

$H$ 는 메시지 인증 키에 해당하고 $X_i$ 는 데이터 블록에 해당합니다. POLYVAL 함수를 거쳐 최종적으로 나온 결괏값 $S_s$ 는 태그 값을 생성하는 데 사용합니다. 식을 잘 보면 결국 $S_s$ 는 메시지 인증 키와 데이터를 사용한 $dot$ 연산 반복으로 생성하는 것을 알 수 있습니다. 그래서 바로 이 $dot$ 연산 부분을 최적화했습니다.

$dot$ 연산은 다항식 $a$ 와 $b$ 의 곱 연산 과정과 $X^{128}$ 의 역원 곱셈 과정, 크게 두 단계로 나눌 수 있습니다. 먼저, $a$ 와 $b$ 의 곱 연산 부분을 그림과 함께 살펴보겠습니다.

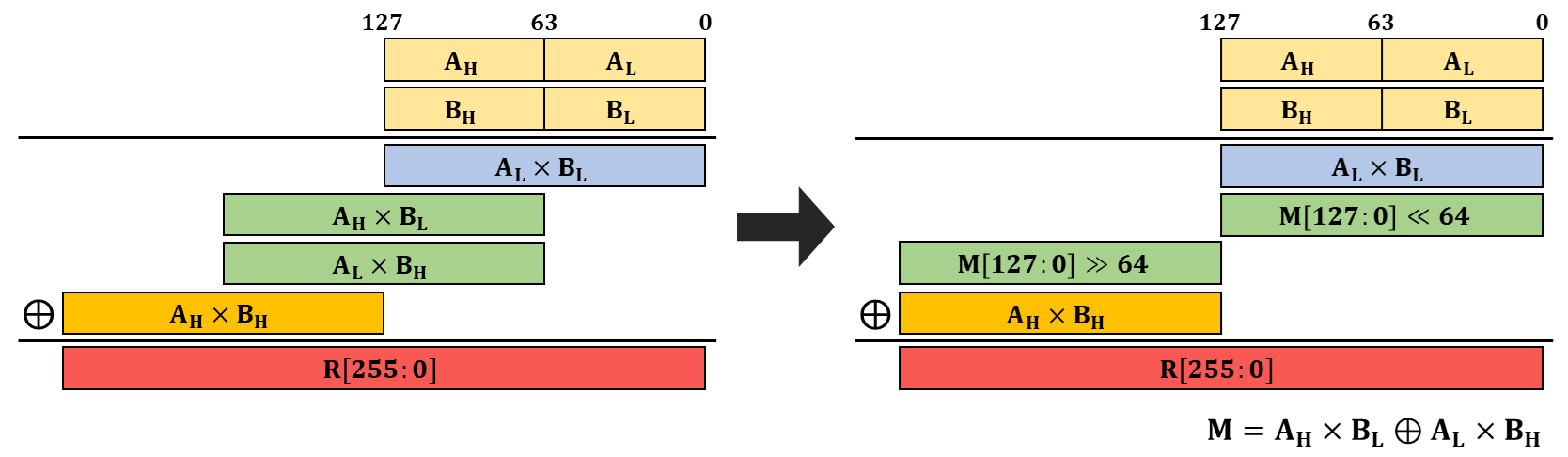
POLYVAL 함수에 정의된 이진 유한체 위에서의 곱셈은 위 그림처럼 표현됩니다. 일반적인 곱셈과 비슷하지만 내부 덧셈 연산을 XOR 형태로 처리하고 캐리가 발생하지 않습니다. 그림에서는 128-bit 곱을 표현했지만 저희가 사용할 이진 유한체 곱셈 명령어는 64-bit 곱셈까지만 제공합니다. 따라서 128-bit 벡터 레지스터 두 개를 입력으로 받아 전체 256-bit를 출력하기 위해서는 이진 유한체 곱셈 명령어를 네 번 호출해야 합니다.

사용할 명령어는 PMULL과 PMULL2입니다. PMULL은 각 피연산자 하위 64-bit 끼리의 곱을, PMULL2는 상위 64-bit 끼리의 곱 연산을 캐리 없이 수행합니다[7]. 128-bit 곱셈을 코드에서는 다음과 같이 표현할 수 있습니다.

LD1.16b {v0}, [%[msg]]  // A = v0
LD1.16b {v1}, [%[key]]  // B = v1

PMULL.1q v2, v0, v1     // v2 = L = AL*BL
PMULL2.1q v5, v0, v1    // v5 = H = AH*BH
EXT.16b v0, v0, v0, #8  // v0 = AH AL to AL AH
PMULL.1q v3, v0, v1     // v3 = AH*BL
PMULL2.1q v4, v0, v1    // v4 = AL*BH
EOR.16b v3, v3, v4      // v3 = M = AL*BL ^ AL*BH

MOV v4.d[0], XZR        // v4 low 64-bit set zero
MOV v4.d[1], v3.d[0]    // v4 = M << 64
MOV v3.d[0], v3.d[1]    // v3 = M >> 64
MOV v3.d[1], XZR        // v3 high 64-bit set zero

EOR.16b v2, v2, v4      // v2 = R[127:0]
EOR.16b v5, v5, v3      // v5 = R[255:128]

다음으로 방금 얻은 두 다항식의 곱셈 결과에 $X^{128}$ 의 역원을 곱해야 합니다. 일반적으로 역원은 확장 유클리드 알고리즘과 같은 방법을 사용해 계산하지만, 여기에서는 복잡한 계산 없이 약간의 수식 전개로 쉽게 해결할 수 있습니다. 방법은 이렇습니다. 위 v2, v5 레지스터에 있는 값은 다항식이 표현된 값이므로 v5를 $h(x)$ 로, v2를 $l(x)$ 로 정의하면 앞선 $a \times b$ 의 결과를 아래와 같이 표현할 수 있습니다.

$\boldsymbol{a \times b=h(x) \times x^{128}+l(x)}$

하지만, 저희가 원하는 계산은 $dot$ 연산의 정의와 같이 양변에 $x^{-128}$ 을 곱한 수식이어야 합니다. 그래서 양변에 $x^{-128}$ 을 곱하면 다음과 같이 정리됩니다.

$\begin{align*}\boldsymbol{a \times b \times x^{-128}}&\boldsymbol{=h(x)+l(x) \times x^{-128}} \\&\boldsymbol{=h(x)+l(x) \times x^{-64} \times x^{-64}}\end{align*}$

이때 $x^{-128}$ 의 곱은 위와 같이 $x^{-64}$ 를 두 번 곱한 것으로 표현할 수 있는데요. $x^{-64}$ 는 다항식 $g(x) = x^{128}+x^{127}+x^{126}+x^{121}+1$ 로부터 아래와 같이 계산할 수 있습니다.

$\begin{align*} \boldsymbol{1} &\boldsymbol{\equiv x^{128}+x^{127}+x^{126}+x^{121}\mod g(x)}\\ \boldsymbol{x^{-64}}&\boldsymbol{\equiv x^{64}+x^{63}+x^{62}+x^{57}\mod g(x)}\\ \end{align*}$

하지만 위 식에서 $l(x) \times x^{-64}$ 계산에 64-bit 곱셈 명령어를 사용하기 위해서는 $x^{-64}$ 를 소거하고 아래와 같이 $x^{64}$ 로 다시 표현해야 합니다.

$\begin{align*}\boldsymbol{l(x) \times x^{-64}}&\boldsymbol{=(l_H(x) \times x^{64}+l_L(x)) \times x^{-64}} \\ &\boldsymbol{=l_H(x)+l_L(x) \times x^{-64}}\\&\boldsymbol{=l_H(x)+l_L(x)(x^{-64}+x^{64}+x^{64})}\\&\boldsymbol{=l_H(x)+l_L(x) \times x^{64}+l_L(x)(x^{-64}+x^{64})}\end{align*}$

이제 거의 다 됐습니다. 앞서 $x^{-64}$ 를 도출한 수식에서 우리는 $x^{64} + x^{-64} \equiv x^{63}+x^{62}+x^{57}$ 을 만들어 낼 수 있습니다. 이때 $x^{63}+x^{62}+x^{57}$ 을 64-bit로 표현하면 $\text{0x}c200000000000000$ 이니 조금 더 정리하면 아래 수식이 완성됩니다.

$\boldsymbol {l(x) \times x^{-64}=l_H(x)+l_L(x) \times x^{64}+l_L(x) \times \text{0x}c200000000000000}$

이 수식을 아래와 같이 그림으로 다시 표현하면 $l(x) \times x^{-64}$ 는 상위 64-bit와 하위 64-bit 자리를 바꿔주고, 곱셈 한 번과 XOR 연산 한 번으로 계산되는 것을 알 수 있습니다.

그래서 최종적으로 $x^{-128}$ 곱셈 연산을 코드로 표현하면 아래와 같습니다.

uint64_t Inverse[2] = {0x0000000000000001, 0xc200000000000000};

LD1.16b {v6}, [%[Inverse]]

// Note1. v5 = h(x) = R[255:128]
// Note2. v2 = l(x) = R[127:0]

// Multiplication x^-64
EXT.16b v2, v2, v2, #8 // l_H l_L to l_L l_H
PMULL2.1q v3, v2, v6   // l_L x 0xc200...00
EOR.16b v2, v2, v3

// Multiplication x^-64
EXT.16b v2, v2, v2, #8 // l_H l_L to l_L l_H
PMULL2.1q v3, v2, v6   // l_L x 0xc200...00
EOR.16b v2, v2, v3

EOR.16b v0, v2, v5     // h(x) + (l(x) * x^-64 * x^-64)

여기까지만 적용해도 꽤 많은 성능 향상을 체감할 수 있습니다. 하지만, 아직 인증 태그 쪽 연산은 개선 여지가 남아 있습니다. 바로 앞서 말씀드린 것처럼 룩업 테이블 방식을 사용하는 것입니다[8]. $S_j$ 수식을 다시 가져와서 조금 더 정리하면 $T=H \times X^{-128}$ 라고 할 때 아래와 같이 표현할 수 있습니다.

$\begin{align*}\boldsymbol{S_j} &\boldsymbol{= dot(S_{j-1}+X_j, H)} \\&\boldsymbol{=(X_j+S_{j-1})\times H \times X^{-128}} \\&\boldsymbol{=(X_j \times H + (X_{j-1}+S_{j-2}) \times HT) \times X^{-128}}\\&\boldsymbol{=(X_j \times H + X_{j-1} \times HT + (X_{j-2}+S_{j-3} \times HT^2))\times X^{-128}}\\&\boldsymbol{=(X_j \times H + X_{j-1} \times HT + X_{j-2} \times HT^2 + (X_{j-3}+S_{j-4})\times HT^3)\times X^{-128}}\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \vdots \end{align*}$

이 수식은 깊이를 어떻게 설정하느냐에 따라 계속 확장할 수 있는데요. 위 식에서 $H, HT, HT^2, HT^3 ...$ 을 사전에 계산해 놓으면 $X^{-128}$ 연산 횟수를 줄일 수 있습니다. 사전 계산값이 없다면 $dot$ 연산 횟수만큼 $X^{-128}$ 곱 연산이 필요하지만, 깊이를 $n$ 으로 하면 $n$ 블록마다 $X^{-128}$ 연산이 한 번 필요합니다.

정리하면, 이 방식은 깊이를 $n$ 으로 정했을 때 기존 $j$ 번의 $X^{-128}$ 연산이 $\frac{j}{n} + n - 1$ 번으로 줄어드는 효과가 있습니다. 이를 위해서는 $16\,n$ 바이트의 메모리와 $n-1$ 번의 $dot$ 연산이 사전에 필요합니다. 즉, 데이터 크기가 클수록 효과가 커지지만 만약 데이터 크기가 작다면 사전 계산에 드는 비용이 더 커질 수 있기 때문에 적용하려는 환경의 데이터 크기를 고려해서 깊이를 조절해야 합니다.

최적화 결과 비교

위와 같은 방법으로 최적화한 코드가 기존 코드와 비교해 성능이 얼마나 많이 향상됐는지 그래프로 간단히 정리해 보았습니다. 그래프 수치를 보면 프로세서별로 적은 양의 데이터는 약 7배, 많은 양의 데이터는 약 30배 가까이 성능이 향상됐다는 것을 알 수 있습니다.

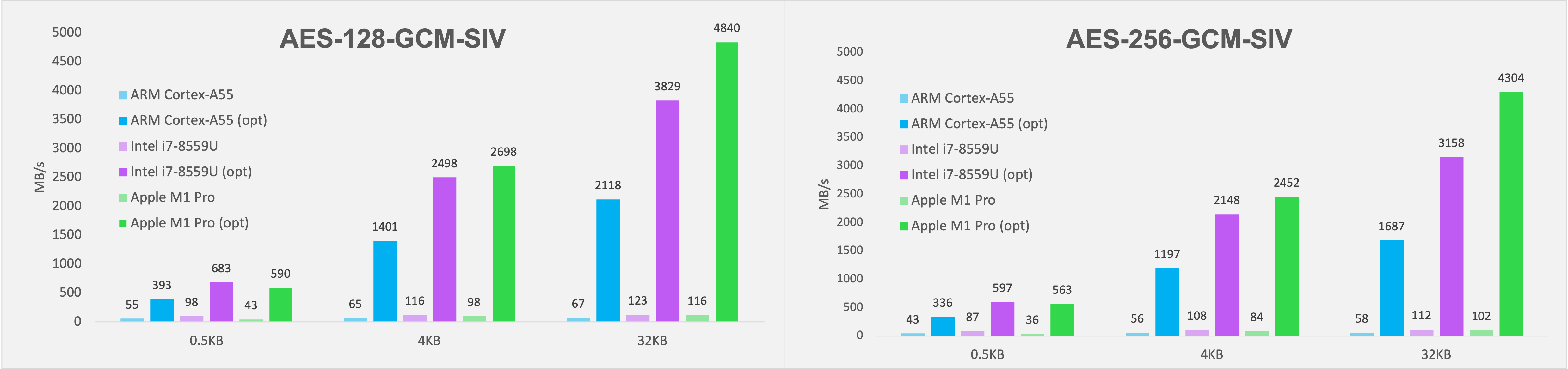
AES-GCM-SIV는 크게 인증 태그 생성 부분과 암호화 부분으로 나뉩니다. 암호화 부분은 데이터 크기에 상관 없이 같은 수치를 보여주지만, 인증 태그 생성 부분은 앞서 말씀드린 것처럼 테이블을 이용한 최적화를 적용했기에 데이터 크기가 작을 때에는 효과가 미미하고 크기가 커질수록 효과가 커집니다. 눈여겨볼 점은 데스크톱 환경뿐만 아니라 Cortex-A55와 같은 모바일 프로세서에서도 성능이 많이 향상됐다는 것입니다. 최근에는 Intel뿐 아니라 ARM 아키텍처 기반 장비들도 AES 명령어와 NEON 명령어를 많이 지원하기 때문에 암호화가 필요한 환경에서 이런 명령어들을 지원한다면 이번 글에서 소개한 방법으로 최적화해 보시는 것도 좋을 것 같습니다.

그 외 개선 사항 및 장점

유지 보수 및 가독성을 위해 내장 함수로 교체

앞서 어셈블리어를 사용해 최적화 작업을 진행했다고 말씀드렸습니다. 몇몇 분들은 글을 읽으면서 이렇게 프로그래밍하면 가독성이 매우 좋지 않고 유지 보수도 어려울 것이라고 생각하셨을 겁니다. 네, 맞습니다. 이 글에 자세히 나와 있지는 않지만 구현할 때는 가용할 수 있는 범위의 레지스터가 몇 개나 있는지, caller-saved 레지스터와 callee-saved 레지스터에는 어떠한 것들이 있는지, 메모리 로드와 저장 과정에서 비효율적인 부분은 없는지 등 고민해야 할 것들이 많은데요. 따라서 지금 당장은 잘 구현했다고 하더라도 나중에 유지 보수하기 위해 코드를 수정하려고 할 때에 많은 어려움이 발생할 것입니다.

이런 문제를 방지하기 위해 어셈블리어로 개발한 코드를 내장(intrinsics) 함수를 사용한 코드로 바꿨습니다. 내장 함수란 각 어셈블리어와 매핑돼 저수준 제어를 직접 할 수 있도록 도와주는 C 함수입니다. 함수처럼 보이지만 실제로는 컴파일 단계에서 인라인 코드 형태로 생성됩니다. 따라서 내장 함수를 사용하면 어셈블리어를 직접 사용할 필요가 없어 프로그래밍 난이도가 많이 줄어들고 컴파일러 도움도 받을 수 있습니다.

아래 표는 AES와 POLYVAL 연산에서 사용하는 주요 명령어에 대응하는 내장 함수입니다[9]. 이외에도 몇 가지 내장 함수를 더 사용하긴 합니다만 해당 작업들은 오픈소스로 공개할 예정이니 궁금하신 분들은 추후 코드가 공개되면 코드에서 확인해 주시기 바랍니다.

2023년 11월에 드디어 오픈소스 AES-GCM-SIV Library를 공개했습니다. AES와 POLYVAL 연산에서 사용하는 주요 명령어에 대응하는 내장 함수에 대해 더 궁금하신 분들은 저희가 공개한 오픈소스에서 확인해 주시기 바랍니다.

Instruction	Return Type	Name	Arguments
AESE	int8x16_t	vaeseq_u8	(uint8x16_t data, uint8x16_t key)
AESMC	int8x16_t	vaesmcq_u8	(uint8x16_t data)
PMULL	poly128_t	vmull_p64	(poly64_t a, poly64_t b)
PMULL2	poly128_t	vmull_high_p64	(poly64x2_t a, poly64x2_t b)

예시 코드처럼 AES-GCM-SIV를 위한 코드 대부분을 내장 함수로 교체했고, 교체한 뒤에도 어셈블리어만을 사용한 구현하고 비슷한 성능을 얻을 수 있었습니다. 결국 성능을 유지하면서 유지 보수와 가독성까지 챙길 수 있었습니다.

uint8x16_t aes128_encrypt(uint8x16_t key[], uint8x16_t block) 
{
	block = vaeseq_u8(block, key[0]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[1]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[2]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[3]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[4]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[5]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[6]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[7]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[8]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[9]);
	block = veorq_u8(block, key[10]);

	return block;
}

AES 명령어를 이용한 구현으로 부채널 공격 내성까지 확보

이번 글에서 살펴본 것처럼 저희는 AES 명령어를 사용해 새롭게 알고리즘을 구현했습니다. 이와 관련해서 앞에서는 성능에 초점을 두고 설명했는데요. 보안 관점에서 말씀드릴 또 다른 장점이 있습니다.

최근에 다양한 암호 구현체를 공격할 때에는 암호학적 분석에 따른 취약점 공격 외에도 흔히 '부채널 공격'이라고 부르는 캐시, 타이밍, 전력 분석, 오류 주입 등의 다양한 공격이 시도되고 있습니다[10][11][12][13]. 따라서 이런 공격에 대한 내성을 갖추는 게 암호 알고리즘뿐 아니라 그 구현체에서도 중요한 평가 대상이 됩니다. 앞서 AES 알고리즘은 일반적으로 룩업 테이블 방식을 사용한다고 말씀드렸습니다. 그런데 그렇게 구현하면 테이블을 참조하기 위한 메모리 접근 시간이 매번 달라지는 현상을 이용한 타이밍 공격과 캐시 기반 공격이 가능해집니다. 이에 따라 최근 많은 오픈소스에서는 AES 알고리즘이 상수 시간으로 작동하도록 다양한 방법을 사용해 구현하고 있습니다[14]. 하지만 일반적으로 안전성과 성능은 서로 상충하는 경우가 많고, 여기서도 예외는 아닙니다. 이와 같이 구현하면 여러 공격에 대한 내성은 생기지만 성능이 많이 저하됩니다. 결국 모든 공격에 전부 대비하는 것은 어렵기 때문에 일반적으로 현실적인 범위 안에서 안전과 성능의 절충점을 찾아 구현하게 됩니다.

그런데 이번 글에서 소개한 AES 명령어를 이용한 구현 방식은 테이블을 참조하지 않고 모든 데이터에 대해 거의 동일한 실행 시간을 보여줍니다. 따라서 타이밍 공격과 캐시 기반 공격 등의 잠재적인 위협 요소에 어느 정도 내성을 갖출 수 있어서 성능 향상뿐 아니라 보안 측면에서도 많은 이점을 얻을 수 있었습니다.

마치며

최근 많은 운영 환경에서 암호 알고리즘을 최적화하기 위한 다양한 하드웨어 자원을 제공합니다. 저희 역시 이를 이용해 AES-GCM-SIV 알고리즘 최적화 작업을 마무리했고 성능을 꽤 많이 향상시켰습니다. 그동안 AES-GCM-SIV가 다른 알고리즘보다 더 안전하긴 하지만 암호 알고리즘 때문에 발생하는 지연 시간이 운영하는 서비스의 가용성에 영향을 미치지 않을까 걱정하시는 개발자분들이 많으셨을 텐데요. 이 글에서 살펴본 것처럼 이제 최적화한 알고리즘을 적용할 수 있으니 그런 걱정은 멈추셔도 되지 않을까 생각합니다.

코드는 오픈소스로 공개할 예정입니다. 더 자세한 내용이 궁금하신 분들은 추후 공개된 오픈소스를 보시면 참고하시면 많은 도움이 될 것이라고 생각합니다. 긴 글 읽어주셔서 감사합니다.

앞서 말씀드렸듯 2023년 11월 AES-GCM-SIV Library라는 이름으로 코드를 오픈소스로 공개했습니다. 더 자세한 내용이 궁금하신 분들은 공개된 오픈소스를 참고하시면 많은 도움이 될 것 같습니다.

참고 문헌

AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption, https://www.rfc-editor.org/rfc/rfc8452.html
Nonce-Disrespecting Adversaries: Practical Forgery Attacks on GCM in TLS, https://www.usenix.org/system/files/conference/woot16/woot16-paper-bock.pdf
Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC, https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-38d.pdf
FIPS 197: Advanced Encryption Standard (AES), https://nvlpubs.nist.gov/nistpubs/fips/nist.fips.197.pdf
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/AESE--AES-single-round-encryption-?lang=en
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/AESMC--AES-mix-columns-?lang=en
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/PMULL--PMULL2--Polynomial-Multiply-Long-?lang=en
Intel® Carry-Less Multiplication Instruction and its Usage for Computing the GCM Mode, https://www.intel.cn/content/dam/www/public/us/en/documents/white-papers/carry-less-multiplication-instruction-in-gcm-mode-paper.pdf
Arm Intrinsics, https://developer.arm.com/architectures/instruction-sets/intrinsics/
Cache-timing attacks on AES, https://cr.yp.to/antiforgery/cachetiming-20050414.pdf
Cache-Collision Timing Attacks Against AES, https://www.iacr.org/archive/ches2006/16/16.pdf
A Simple Power-Analysis (SPA) Attack on Implementations of the AES Key Expansion, https://link.springer.com/chapter/10.1007/3-540-36552-4_24
Power analysis attacks on the AES-128 S-box using Differential power analysis (DPA) and correlation power analysis (CPA), https://www.tandfonline.com/doi/full/10.1080/23742917.2016.1231523
Faster and Timing-Attack Resistant AES-GCM, https://eprint.iacr.org/2009/129.pdf

Security

Blog