This post is also available in the following languages. Japanese, Korean

How we optimized the AES-GCM-SIV encryption algorithm

Juhong Han2023-09-21

In charge of security technology research and security consulting in the Security R&D team.

Hello, this is Juhong Han, who is in charge of security research and consulting in the Security R&D team. There are various security technologies in the world, and among them, cryptographic algorithms are essential for data security. LINE also applies various cryptographic algorithms to protect sensitive data when providing services. And in our team, we are developing cryptographic libraries to make it easier to use for other LINE developers who are not used to cryptographic algorithms.

AES-GCM-SIV is one of them. Currently, AES-GCM-SIV is available in several libraries like Tink and BoringSSL. However, when our team first adopted it, this algorithm was not supported yet by these libraries, so our team had to implement it in C. And after implementing it we wrapped it to various environments like Java, Android, and Go to make it easier to use for other teams. As a result, now it is used in several server-side projects, as well as in the LINE client (Android and iOS) for the message sticker encryption.

As it's being used by more and more teams, we saw the need to optimize it for the widely used ARM environment. In this post, I'll share the process of optimizing it for the ARM environment and the results of our efforts.

What is AES-GCM-SIV?
- Structure of the algorithm
- Pros and cons
How we optimized it
- The optimization process
- Comparing optimization results
Other improvements and advantages
- Replacing assembly language code with intrinsic functions for better maintainability and readability
- Defending against side-channel attacks with an AES instruction implementation
Conclusion
- References used

What is AES-GCM-SIV?

If you're interested in information security, you probably know that AES-GCM is one of the most popular authenticated encryption algorithms, but AES-GCM-SIV[1] may be unfamiliar to you. It's essentially an algorithm that improves the security of the original GCM mode slightly. The original GCM mode has a vulnerability when reusing the same key and nonce pair to encrypt two different pieces of data[2]. Although it's recommended not to reuse the same key and nonce pair[3], users who are unaware of this can misuse it, which would damage encrypted data. AES-GCM-SIV is an algorithm designed to resist this issue. Now let's take a look at its structure and the pros and cons for readers who are not familiar with AES-GCM-SIV yet.

Structure of the algorithm

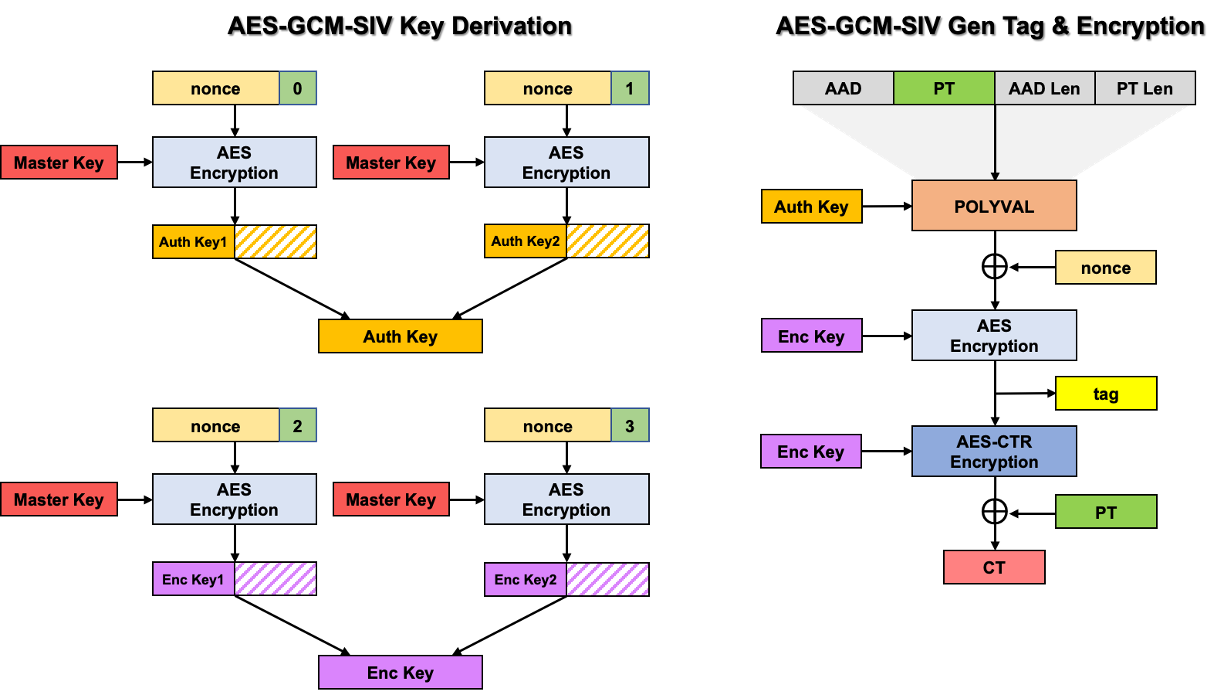
AES-GCM-SIV can be broadly divided into three phases: key derivation, message authentication, and message encryption. During the initial phase of the algorithm, the key derivation function takes the master key as input and generates the message authentication and encryption keys. Then, an authentication tag is generated through the POLYVAL and AES algorithms. In the final phase, the message is encrypted using the tag as a counter value. The separate creation of authentication and encryption keys at the start, and the calculation of the authentication value before using it as a counter to bind to the ciphertext, makes AES-GCM-SIV more secure than the previous GCM mode.

Pros and cons

Like any cryptographic algorithm, AES-GCM-SIV also has its own advantages and disadvantages.

Advantages

The first advantage is it has strong security. As mentioned earlier, the main idea of AES-GCM-SIV is to generate encryption and authentication keys separately using a master key for encrypting/decrypting messages. These keys are generated as sufficiently long key streams that look like random numbers. And these key streams which resemble randomized output, make it harder for an attacker to predict.

Furthermore, if the encryption or authentication key is exposed to an attacker, AES-GCM-SIV doesn't propagate any problems to the other keys or the master key. The authentication and encryption key pair can be simply re-derived with new nonces. In contrast, other common algorithms usually use the master key directly without a key derivation process. Of course, other algorithms may have a similar structure if the protocol is well designed, but AES-GCM-SIV has this built-in from the start, it has a significant advantage by minimizing mistakes even for users who are not familiar with designing security protocols.

Another security-related advantage is its resistance to nonce reuse issues that have occurred in traditional authenticated encryption algorithms. In the standard GCM mode, if an attacker gets hold of a pair of ciphertext and plaintext created with the same key and nonce, they can also recover the remaining plaintext. In such a scenario, the authentication key can be easily compromised, allowing the attacker to generate as many pairs of plaintext, ciphertext, and authentication tags as they want. In contrast, with AES-GCM-SIV, even in the same situation, the attacker can only determine whether two pieces of data were encrypted with the same data, without gaining any other information. Ideally, this information shouldn't be accessible to the attacker, but this is an inevitable limitation in deterministic algorithms.

The second advantage is the ability to utilize various hardware resources when implementing the algorithm. As shown in the diagram, AES-GCM-SIV uses the AES algorithm internally for encryption, decryption, and key generation. Since the AES algorithm has been widely used for a long time globally, many CPUs now come with hardware accelerators for AES that significantly outperform software implementations. Moreover, the POLYVAL function used for generating the authentication tag requires operations on a binary finite field. Fortunately, many modern CPUs provide dedicated instruction sets, such as carry-less multiplication, specifically designed for this purpose. As a result, AES-GCM-SIV can utilize various hardware resources for the compute authentication and encryption/decryption processes. Additionally, the formula used in POLYVAL is designed to be similar to the one used in GCM mode and computed more efficiently on a little-endian architecture. Consequently, this leads to another benefit that the GHASH implementation of GCM can be reused within the POLYVAL algorithm.

Disadvantages

Now let's look at the disadvantages. As you may have already noticed, due to the secure structure we highlighted as an advantage, it performs slightly less efficiently than other algorithms when implemented as software. Since the authentication and encryption keys are regenerated each time during the encryption/decryption process, the performance is inevitably lower than other algorithms that store the initially generated round key and reuse it multiple times.

Another downside is that, due to the algorithm's structure, it can't process data in a stream. This is because the additional authentication data (AAD) and the authentication process for the plaintext and ciphertext must be carried out before the encryption/decryption process. Since it can't handle data in a stream, all data and memory resources must be available before starting the encryption/decryption process.

However, since these are performance-related drawbacks, they can be compensated by using hardware accelerators and specific instruction sets.

How we optimized it

As mentioned earlier, when implementing the AES-GCM-SIV algorithm we can take advantage of the AES hardware accelerators and special instruction sets for GCM mode. Our team's previous library used MbedTLS source code and was optimized exclusively for the Intel x86-64 architecture. However, considering the increasing use by other teams and the fact that most of our devices are now based on the ARM architecture, we decided that optimization for the ARM environment is also necessary. Of course, we only adopt ARMv8-A CPUs that supported cryptographic hardware accelerators, but most modern ARM CPUs meet that specification.

Implementing on an x86-64 environment is essentially the same as on an ARM environment, with only minor differences in the instruction set. Therefore, in this post, we'll solely focus on the implementation in the ARM environment.

The optimization process

The typical optimization process involves writing the source code, using profiling tools to identify areas that need optimization, and then concentrating on optimizing those specific parts. In this case, however, the optimization target was clear: the encryption and data authentication processes within the AES-GCM-SIV algorithm, so we focused on optimizing those parts without specific profiling.

Generally, optimization is often achieved by programming with suitable data types, syntax, and algorithms, which can then be further optimized by the compiler using certain techniques. However, when optimizing cryptographic algorithms, there are several areas where compiler optimizations fall short. Cryptographic operations require optimization in many areas - from handling carry in various mathematical operations to optimizing vector operations, configuring pipelining per CPU architecture, and controlling registers for data loading and storing. These aspects are too complex for the compiler to fully optimize. Therefore, many cryptographic engineers resort to assembly language to optimize these parts. Although assembly language is more challenging to program and takes longer to develop, it has the advantage of utilizing hardware resources as efficiently as possible. We also used assembly language in our development. Let's examine how we optimized it.

The AES structure and instructions

As mentioned earlier, in order to optimize AES-GCM-SIV, we have to optimize the AES algorithm used internally. Although we used a hardware accelerator, the optimizations we'll explain are also relevant to the AES structure, so we'll keep it brief (the details of each step are described in the FIPS-197[4] document, so please refer to that).

AES can be divided into two parts: key expansion and encryption/decryption. The key expansion part involves generating the round key used at each round's final stage in the encryption process. A single round key is made from four 32-bit words. The encryption process is structured as illustrated below, with the MixColumns operation missing in the last round. It's crucial to note that while the encryption key size can be 128, 192, or 256 bits, all the round keys produced are 128 bits to fit the block size.

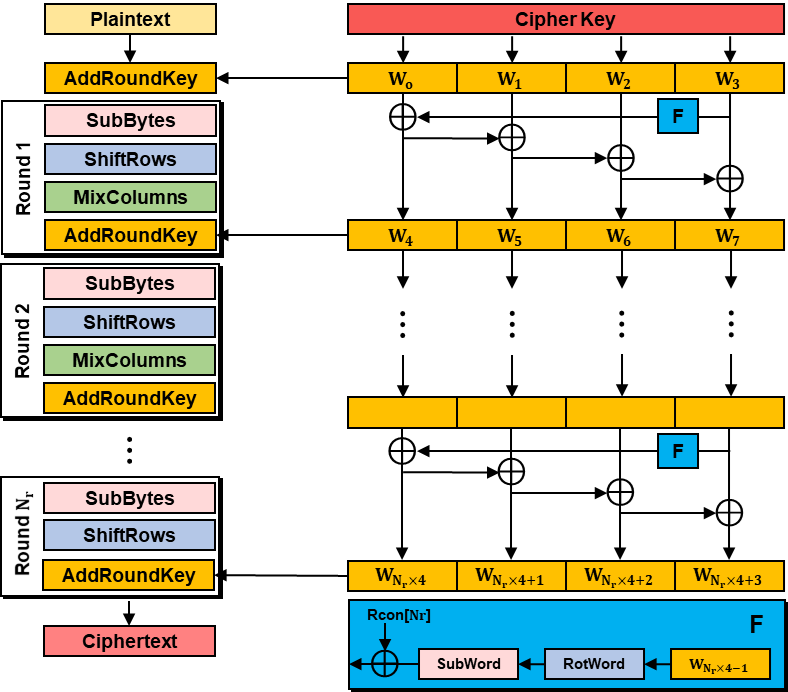
Now let's look at the AES-specific instruction set to be used on the ARM architecture. As mentioned earlier, AES-GCM-SIV doesn't use the AES decryption function because it uses the CTR mode internally. Therefore, there are only two instructions that are used[5][6].

AESE - AES single round encryption

AddRoundKey, SubBytes, ShiftRows are processed as follows.

AESE <Vd>.16B, <Vn>.16B
{
	bits(128) operand1 = v[d];
	bits(128) operand2 = v[n];
	bits(128) result;

	result = operand1 EOR operand2;
	result = AESSubBytes(AESShiftRows(result));

	v[d] = result;
}

AESMC - AES MixColumns
- Handles remaining MixColumns calculations.

Key expansion process

The key expansion process didn't take up much of the overall operation time. However, when considering that AES-GCM-SIV performs the key expansion process multiple times for each encryption, we determined that it would be worth optimizing if there could be improvements from a long-term usage perspective.

The lookup table approach is often used when optimizing cryptographic algorithms. This approach replaces heavy computational tasks with simple table lookups, using additional memory. AES software implementations also use this method to cut down on computation. If you check out open-source AES implementations, you'll typically find an array called S-Box. This S-Box (substitution table) is linked to the SubBytes transformation during the encryption process. It's used for both the SubWord in the key expansion process and the SubBytes in the encryption process.

As we've seen in the previous AES scheme, the key expansion process involves applying the RotWord and SubWord to the last word of the previous round key. Essentially, the RotWord and SubWord are the same as ShiftRows and SubBytes in the encryption part, but they're only applied to one word. So, even though there aren't any special instructions for the key expansion process, we can still optimize it using the instructions used in the encryption process.

	LDR W0, ="#RCON"
	MOV W15, W12
	DUP v1.4s, W15
	EOR.16b v0, v0, v0
	AESE v0.16b, v1.16b
	UMOV W15, v0.s[0]
	ROR W15, W15, #8
	EOR W9, W9, W15
	EOR W9, W9, W0
	EOR W10, W10, W9
	STP W9, W10, [%[rk]], #8
	EOR W11, W11, W10
	EOR W12, W12, W11
	STP W11, W12, [%[rk]], #8

In the code above, the value of the last word from the previous round key is stored in W15. This value is then copied to every word position in the v1 vector register using the DUP instruction. Afterward, it's finalized through some bit operations, using the output value of the AESE instruction. One important aspect of this implementation is that the EOR instruction is called before the AESE. The EOR instruction results in a XOR operation if the input registers are identical, yielding a result of 0. Essentially, this sets the value to 0, eliminating the AddRoundKey process. Using the EOR instruction to initialize variables is a common practice in assembly language programming, so it's a handy trick to remember when examining other code.

Lastly, we initialize the value of Vd to zero after the AESE operation, then the result is as follows.

AESE Vd, Vn 
{
	operand1 = Vd;
	operand2 = Vn;
	result;

	operand2 = operand1 EOR operand2; // operand2 = 0 EOR operand2;
	result = AESSubBytes(AESShiftRows(operand2));

	vd = result;
}

Since the AESE instruction starts with an XOR operation between operand1 and operand2, if Vd does not hold a zero, it will result in input for the subsequent ShiftRows and SubBytes different from operand2.

Encryption process

Like the key expansion process, the encryption process is usually implemented using a lookup table approach. This table holds the results of the pre-computed SubBytes, ShiftRows, and MixColumns operations. So, the encryption process involves a table reference and a few bit operations to XOR with the round key.

However, you can skip the lookup table by using dedicated AES instructions. This way, a single round of encryption can be done in roughly 6 cycles, depending on the processor. As a result, we don't need to use a lookup table. If you're interested in the actual implementation, I've written a code for 128-bit key encryption.

	// Load plaintext
	LD1.16b {v0}, [%[in]]
	
	// Load roundkeys
	LD1.16b {v1-v4}, [%[rk]], #64

	// 1 to 4 round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v3.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v4.16b
	AESMC v0.16b, v0.16b

	// Load roundkeys
	LD1.16b {v1-v4}, [%[rk]], #64

	// 5 to 8 round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v3.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v4.16b
	AESMC v0.16b, v0.16b
	
	// Load roundkeys
	LD1.16b {v1-v3}, [%[rk]]

	// 9 to last round encryption
	AESE v0.16b, v1.16b
	AESMC v0.16b, v0.16b
	AESE v0.16b, v2.16b

	// Last AddRoundKey
	EOR.16b v0, v0, v3

	// Store ciphertext
	ST1.16b {v0}, [%[out]]

If you examine the code, you'll notice that the V0 register holds the plaintext, while registers v1 to v4 load four round keys at once for each round of encryption. Of course, this is just an example, and the number of loaded round keys and used vector registers may vary depending on the design. But did you spot something odd about the code? It doesn't quite align with the structure we discussed earlier.

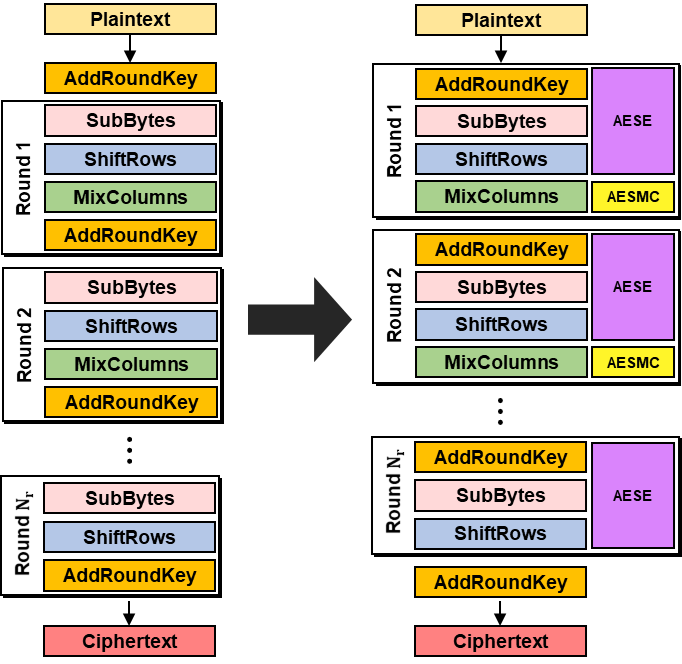
In the AES standard documentation, each round is designed in this order: SubBytes, ShiftRows, MixColumns, AddRoundKey. The last round skips the MixColumns step. However, this doesn't match the inner process of the AESE instruction.

Despite this, the process makes sense if you think of it as shown in the figure below. For the final round, we just need to call the AESE instruction and go through the AddRoundKey process with an XOR operation, as shown in the code.

Tag generation process

Now, let's discuss optimizing the tag generation process. The AES-GCM-SIV algorithm uses a Galois field-based authentication mechanism, just like the GCM mode. We refer to it as POLYVAL. This is essentially the reversed order of the coefficients of the irreducible polynomial of the GHASH for GCM mode[1]. It's more efficiently computed in a little-endian environment. Because the expression below is defined over a binary field, the POLYVAL operation also needs addition, subtraction, multiplication, and inverse operations over a binary field.

$\begin{align*} \textbf{Polynomial of AES-GCM-SIV} &\boldsymbol{:x^{128}\boldsymbol{+}x^{127}+x^{126}+x^{121}+1}\\\textbf{Polynomial of GCM} &\boldsymbol{:x^{128}+x^7+x^2+x+1}\end{align*}$

I will briefly look into the representation and operations over a binary field for those who are unfamiliar with them. In a binary polynomial, each term is composed of coefficients that are either 0 or 1. Think of this as similar to how computers represent each bit as 0 or 1. For example, polynomial $x^7+x^2+x+1$ can be represented by $10000111_{(2)}$ .

This way, even with higher degrees, all terms can fit within the array. Moreover, operations over a binary field have a unique feature where carries aren't propagated. So, addition and subtraction operations are done using XOR between each operand. Similarly, multiplication operations are a bit like regular multiplication, but the addition step during multiplication is handled using XOR without carry propagation.

Now, let's talk about the definition of the POLYVAL function and how to optimize it. The definition of the POLYVAL function is as follows[1].

$\\\boldsymbol{Polyval(H,X_1,X_2,\dots,X_s)=S_s}\textbf{,}\\\textbf{where }\boldsymbol{S_j = }\begin{cases}\boldsymbol{0}&\textbf{if }\boldsymbol{j = 0}\\\boldsymbol{dot(S_{j-1}+X_j,H)}&\textbf{if }\boldsymbol{1\le j\le s} \textbf{,}\\\end{cases}\\\textbf{and }\boldsymbol{dot(a,b)=a \times b \times X^{-128}}$

$H$ is the message authentication key and $X_i$ is the data block. The final result of the POLYVAL function $S_s$ is used to compute the tag value. If you look more closely, you can figure out that $S_s$ is generated by iterating on the $dot$ operation with the message authentication key and data. So we optimized the $dot$ operation part.

The $dot$ operation can be described in two parts: the polynomial multiplication of $a$ and $b$ , and the inverse multiplication of $X^{128}$ . First, let's look at the polynomial multiplication of the $a$ and $b$ parts with an illustration.

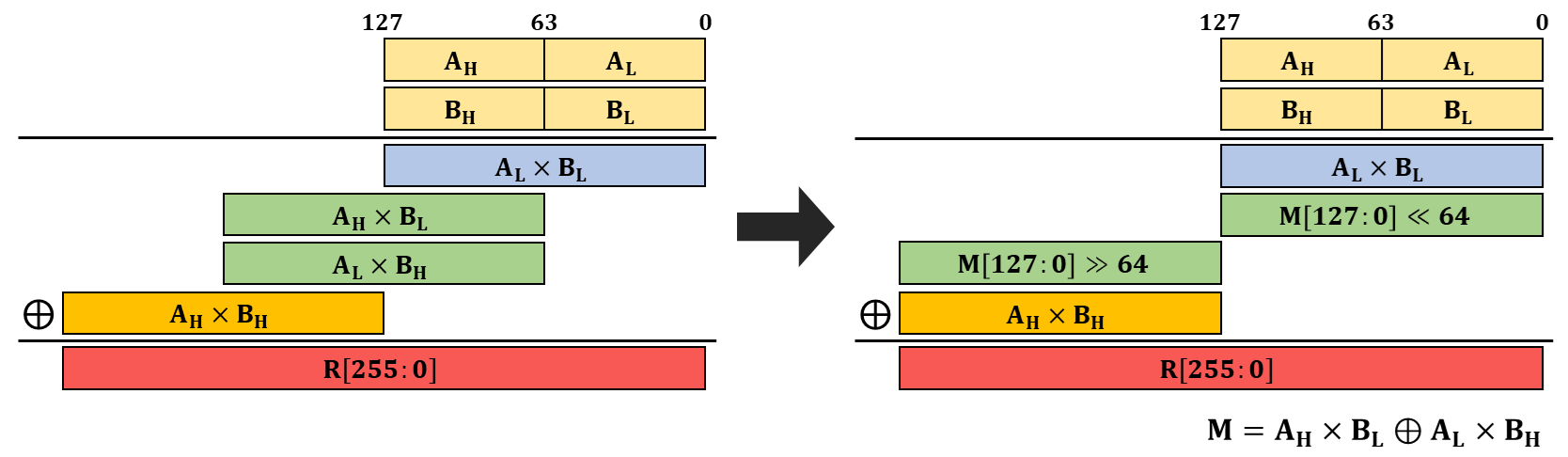
The multiplication over a binary field, as defined in the POLYVAL function, is shown in the figure above. It's like regular multiplication, but the internal addition is computed as an XOR without any carry propagation. The figure shows a 128-bit multiplication, but the binary field multiplication instructions we'll use only offer up to 64-bit multiplication. Therefore, to take two 128-bit vector registers as input and output a full 256-bit, we need to call the binary field multiplication instruction four times.

The instructions we'll use are PMULL and PMULL2. PMULL computes the multiplication of the lower 64 bits of each operand, while PMULL2 computes the multiplication of the upper 64 bits without any carry[7]. Therefore, a 128-bit multiplication can be represented in code as follows.

LD1.16b {v0}, [%[msg]]  // A = v0
LD1.16b {v1}, [%[key]]  // B = v1

PMULL.1q v2, v0, v1     // v2 = L = AL*BL
PMULL2.1q v5, v0, v1    // v5 = H = AH*BH
EXT.16b v0, v0, v0, #8  // v0 = AH AL to AL AH
PMULL.1q v3, v0, v1     // v3 = AH*BL
PMULL2.1q v4, v0, v1    // v4 = AL*BH
EOR.16b v3, v3, v4      // v3 = M = AL*BL ^ AL*BH

MOV v4.d[0], XZR        // v4 low 64-bit set zero
MOV v4.d[1], v3.d[0]    // v4 = M << 64
MOV v3.d[0], v3.d[1]    // v3 = M >> 64
MOV v3.d[1], XZR        // v3 high 64-bit set zero

EOR.16b v2, v2, v4      // v2 = R[127:0]
EOR.16b v5, v5, v3      // v5 = R[255:128]

Next, we have to multiply the result of each polynomial's multiplication by the inverse of $X^{128}$ . The inversion is usually calculated using methods such as the Extended Euclidean algorithm, but in this case, we can derive it without complex calculations. Let's explore how we can do this. The values stored in the v2 and v5 registers represent polynomials. So, If we define v5 as $h(x)$ and v2 as $l(x)$ , we can express the result of $a \times b$ as follows.

$\boldsymbol{a \times b=h(x) \times x^{128}+l(x)}$

However, the calculation we want should be a formula where both sides are multiplied by $x^{-128}$ , like the definition of the $dot$ operation. Therefore, upon multiplying both sides by $x^{-128}$ , we can represent it as follows.

$\begin{align*}\boldsymbol{a \times b \times x^{-128}}&\boldsymbol{=h(x)+l(x) \times x^{-128}} \\&\boldsymbol{=h(x)+l(x) \times x^{-64} \times x^{-64}}\end{align*}$

The multiplication of $x^{-128}$ can be represented as $x^{-64}$ multiplied twice, as shown above. And $x^{-64}$ can be derived from the polynomial $g(x) = x^{128}+x^{127}+x^{126}+x^{121}+1$ as follows.

$\begin{align*} \boldsymbol{1} &\boldsymbol{\equiv x^{128}+x^{127}+x^{126}+x^{121}\mod g(x)}\\ \boldsymbol{x^{-64}}&\boldsymbol{\equiv x^{64}+x^{63}+x^{62}+x^{57}\mod g(x)}\\ \end{align*}$

However, in order to use the 64-bit multiplication instruction to calculate $l(x) \times x^{-64}$ in the above equation, we have to eliminate the $x^{-64}$ and represent it as $x^{64}$ as shown below.

$\begin{align*}\boldsymbol{l(x) \times x^{-64}}&\boldsymbol{=(l_H(x) \times x^{64}+l_L(x)) \times x^{-64}} \\ &\boldsymbol{=l_H(x)+l_L(x) \times x^{-64}}\\&\boldsymbol{=l_H(x)+l_L(x)(x^{-64}+x^{64}+x^{64})}\\&\boldsymbol{=l_H(x)+l_L(x) \times x^{64}+l_L(x)(x^{-64}+x^{64})}\end{align*}$

We're almost done. From the equation we derived for $x^{-64}$ earlier, now we can derive $x^{64} + x^{-64} \equiv x^{63}+x^{62}+x^{57}$ . And, if we represent $x^{63}+x^{62}+x^{57}$ in 64 bits, then we can denote it as $\text{0x}c200000000000000$ . Therefore if we simplify, then we can derive the equation as follows.

$\boldsymbol {l(x) \times x^{-64}=l_H(x)+l_L(x) \times x^{64}+l_L(x) \times \text{0x}c200000000000000}$

Representing this formula as an illustration again, $l(x) \times x^{-64}$ swaps the high and low 64-bit digits, and is computed as one multiplication and one XOR operation.

So the final code representation of the $x^{-128}$ multiplication is as follows.

uint64_t Inverse[2] = {0x0000000000000001, 0xc200000000000000};

LD1.16b {v6}, [%[Inverse]]

// Note1. v5 = h(x) = R[255:128]
// Note2. v2 = l(x) = R[127:0]

// Multiplication x^-64
EXT.16b v2, v2, v2, #8 // l_H l_L to l_L l_H
PMULL2.1q v3, v2, v6   // l_L x 0xc200...00
EOR.16b v2, v2, v3

// Multiplication x^-64
EXT.16b v2, v2, v2, #8 // l_H l_L to l_L l_H
PMULL2.1q v3, v2, v6   // l_L x 0xc200...00
EOR.16b v2, v2, v3

EOR.16b v0, v2, v5     // h(x) + (l(x) * x^-64 * x^-64)

Even with just these optimizations, you'll notice significant performance improvements. However, there's still room to improve the authentication tag operations. This involves using the lookup table approach[8]. If we take the $S_j$ equation again and refine it to $T=H \times X^{-128}$ , it can be expressed as follows.

$\begin{align*}\boldsymbol{S_j} &\boldsymbol{= dot(S_{j-1}+X_j, H)} \\&\boldsymbol{=(X_j+S_{j-1})\times H \times X^{-128}} \\&\boldsymbol{=(X_j \times H + (X_{j-1}+S_{j-2}) \times HT) \times X^{-128}}\\&\boldsymbol{=(X_j \times H + X_{j-1} \times HT + (X_{j-2}+S_{j-3} \times HT^2))\times X^{-128}}\\&\boldsymbol{=(X_j \times H + X_{j-1} \times HT + X_{j-2} \times HT^2 + (X_{j-3}+S_{j-4})\times HT^3)\times X^{-128}}\\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \vdots \end{align*}$

This formula can be extended based on the chosen nested level. By precomputing $H, HT, HT^2, HT^3 ...$ and creating a table, we can reduce the number of $X^{-128}$ operations. Without a precomputed table, $X^{-128}$ multiplication operations are required for each $dot$ operation. However, if we set the nested level to $n$ and create a precomputed table, only one $X^{-128}$ operation is required for every $n$ blocks.

In summary, by using this approach, the effect is that initial $j$ operations are reduced to $\frac{j}{n} + n - 1$ when the nested level is set to $n$ . This requires $16\,n$ bytes of memory and $n-1$ $dot$ operations. Notably, the impact is greater with larger data sizes. However, it's important to note that for smaller data sizes, the cost of precomputation might be relatively higher. Therefore, it's advisable to adjust the nested level to align with the data size that fits into your environment.

Comparing optimization results

Let's examine the graph to see how much the optimized code has improved in terms of performance compared to the original code. From the values displayed on the graph, it's evident that we achieved performance improvements of approximately 7 times for smaller data sizes and nearly 30 times for larger data sizes, for each processor.

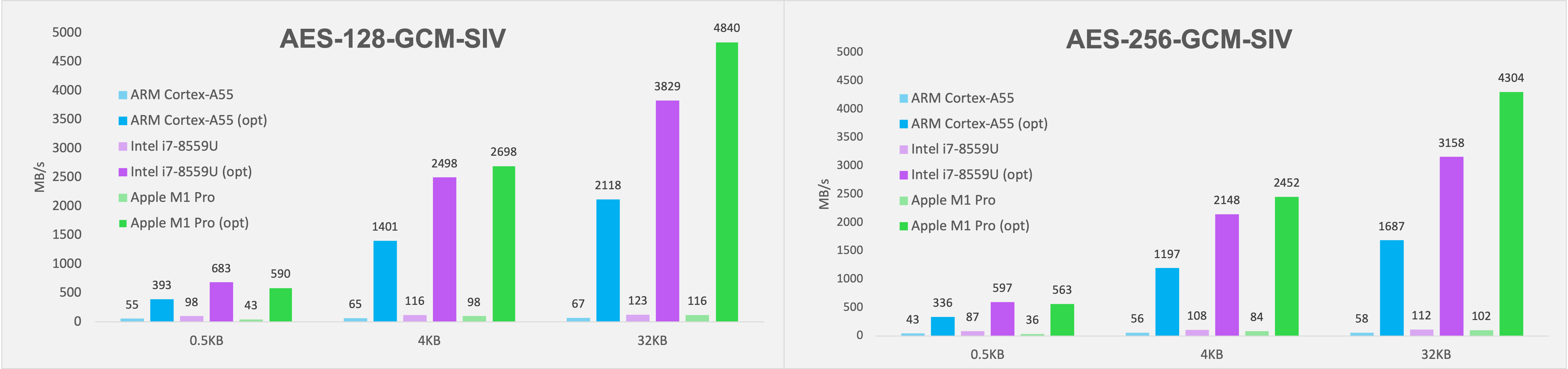
AES-GCM-SIV can be broadly divided into two parts: generating the authentication tag and encryption. The encryption part performs the same regardless of data size, but as mentioned earlier, the authentication tag generation part is optimized using lookup tables, so its effectiveness is minimal with small data and increases as the data size grows. It's worth noting that performance has significantly improved not just in desktop environments, but also in mobile processors like the Cortex-A55. Lately, many devices based on ARM architecture, not just Intel, support AES and NEON instructions. So, if you're in an environment that needs encryption and supports these instructions, you might want to try optimizing using the method outlined in this post.

Other improvements and advantages

Replacing assembly language code with intrinsic functions for better maintainability and readability

I previously mentioned that we used assembly language for optimization. Some of you might have thought that this approach to programming could result in poor readability and difficulty in maintenance. You're correct. This post doesn't detail everything, but during implementation, we have to consider many things. For instance, how many available registers are there, what are the caller-saved and callee-saved registers, and are there any inefficiencies in memory loading and saving procedures. So, even if we implement it well now, it'll be challenging to modify and maintain the code later.

To avoid these problems, we switched the code developed in assembly language to code using intrinsic functions. Intrinsic functions are C functions that map to assembly language, allowing direct low-level control. They might seem like regular functions, but they're actually created as inline code during the compile stage. Hence, using intrinsic functions eliminates the need to directly use assembly language, significantly reducing programming complexity and allowing for compiler assistance.

The table below shows the intrinsic functions that correspond to the main instructions used in AES and POLYVAL operations[9]. We're using a few more intrinsic functions, but those interested can check them out once we release our open-source code.

In November 2023, we finally released the open-source AES-GCM-SIV Library. If you're curious about the built-in functions corresponding to the main commands used in AES and POLYVAL operations, please check them out in our open-source release.

Instruction	Return Type	Name	Arguments
AESE	int8x16_t	vaeseq_u8	(uint8x16_t data, uint8x16_t key)
AESMC	int8x16_t	vaesmcq_u8	(uint8x16_t data)
PMULL	poly128_t	vmull_p64	(poly64_t a, poly64_t b)
PMULL2	poly128_t	vmull_high_p64	(poly64x2_t a, poly64x2_t b)

We replaced much of the code with intrinsic functions like the example code. And even after the replacement, we were able to achieve comparable performance to an assembly-only implementation. Ultimately, we were able to maintain performance while also ensuring both maintainability and readability.

uint8x16_t aes128_encrypt(uint8x16_t key[], uint8x16_t block) 
{
	block = vaeseq_u8(block, key[0]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[1]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[2]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[3]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[4]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[5]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[6]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[7]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[8]);
	block = vaesmcq_u8(block);

	block = vaeseq_u8(block, key[9]);
	block = veorq_u8(block, key[10]);

	return block;
}

Defending against side-channel attacks with an AES instruction implementation

As discussed in this post, we've implemented the AES-GCM-SIV algorithm using AES instructions. While we've previously focused on performance, there's another advantage to discuss from a security standpoint.

Recently, when attacking various cryptographic implementations, not only are vulnerabilities targeted based on cryptographic analysis, but various attacks, commonly referred to as "side-channel attacks," are also attempted. These include cache attacks, timing attacks, power analysis, fault injection, and more[10][11][12][13]. Therefore, resistance to these attacks is a crucial evaluation point, not just for the cryptographic algorithms themselves, but also for their implementations.

We mentioned earlier that the AES algorithm typically uses a lookup table approach. However, this implementation can lead to timing attacks and cache-based attacks because the memory access time to reference the table can vary. To mitigate these issues, many recent open-source projects have implemented the AES algorithm to operate in constant time[14].

However, safety and performance often conflict, and this situation is no exception. While this implementation can make you resistant to many attacks, it can significantly degrade performance. Since it's challenging to prepare for every possible attack, we usually end up finding a compromise between safety and performance that's realistic.

However, the AES implementation we've introduced in this post, which uses the AES instruction set, doesn't reference tables and displays almost the same execution time for all data. This method provides some resistance to potential threats like timing attacks and cache-based attacks. As a result, we've been able to reap significant benefits in terms of both performance and security.

Conclusion

Nowadays, many operating environments offer various hardware resources to optimize cryptographic algorithms. We've utilized these resources to optimize our AES-GCM-SIV algorithm, resulting in a significant performance boost. Even though AES-GCM-SIV is safer than other algorithms, many developers might have been worried about the potential impact of the latency caused by cryptographic algorithms on their services' availability. But as we've seen in this post, you can now apply the optimized algorithm and put those worries to rest.

We plan to release the code as open source. If you're keen to learn more, referring to the upcoming open-source release should prove helpful. Thanks for taking the time to read this lengthy post.

As I mentioned earlier, in November 2023, we released the code as open-source under the name AES-GCM-SIV Library. If you're interested in more details, referring to the released open-source will be very helpful.

References used

AES-GCM-SIV: Nonce Misuse-Resistant Authenticated Encryption, https://www.rfc-editor.org/rfc/rfc8452.html
Nonce-Disrespecting Adversaries: Practical Forgery Attacks on GCM in TLS, https://www.usenix.org/system/files/conference/woot16/woot16-paper-bock.pdf
Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC, https://nvlpubs.nist.gov/nistpubs/Legacy/SP/nistspecialpublication800-38d.pdf
FIPS 197: Advanced Encryption Standard (AES), https://nvlpubs.nist.gov/nistpubs/fips/nist.fips.197.pdf
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/AESE--AES-single-round-encryption-?lang=en
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/AESMC--AES-mix-columns-?lang=en
Arm A64 Instruction Set Architecture, https://developer.arm.com/documentation/ddi0596/2021-12/SIMD-FP-Instructions/PMULL--PMULL2--Polynomial-Multiply-Long-?lang=en
Intel® Carry-Less Multiplication Instruction and its Usage for Computing the GCM Mode, https://www.intel.cn/content/dam/www/public/us/en/documents/white-papers/carry-less-multiplication-instruction-in-gcm-mode-paper.pdf
Arm Intrinsics, https://developer.arm.com/architectures/instruction-sets/intrinsics/
Cache-timing attacks on AES, https://cr.yp.to/antiforgery/cachetiming-20050414.pdf
Cache-Collision Timing Attacks Against AES, https://www.iacr.org/archive/ches2006/16/16.pdf
A Simple Power-Analysis (SPA) Attack on Implementations of the AES Key Expansion, https://link.springer.com/chapter/10.1007/3-540-36552-4_24
Power analysis attacks on the AES-128 S-box using Differential power analysis (DPA) and correlation power analysis (CPA), https://www.tandfonline.com/doi/full/10.1080/23742917.2016.1231523
Faster and Timing-Attack Resistant AES-GCM, https://eprint.iacr.org/2009/129.pdf

Security

Blog