これはLINE Advent Calendar 2018の14日目の記事です。
LINEの上村です。今日は文字列です。
はじめに
トライ (trie)は文字列の集合を索引化し高速な検索を可能にするデータ構造であり、領域効率や高速性を向上させた多様なアルゴリズムが提案され種々の実装が公開されています。 IPアドレスの検索、形態素解析器における辞書からの候補の列挙、キー入力時のオートコンプリートといった有益な応用があり、文字列業界以外でもご存知の方は多いかもしれません。
この記事で紹介するsftrieは簡単で効率よい新たなトライ表現とそのC++実装です。
主な特徴は以下の通りです:
- 大きなアルファベットをサポートします。また、いわゆるNULL文字も必要としないため、バイト列やASCIIコードからUnicode、単語等に割り振ったIDのような一般の整数まで、様々な値を文字型として扱えます
- ノード探索順の工夫に基づいたトライ表現により、単純な構造ながら比較的良好な性能を実現します。日本語テキストの場合、UTF-8の代わりにUTF-16を用いることでサイズ・速度共にさらに改善できます
実際のデータ構造の例を下に示します。
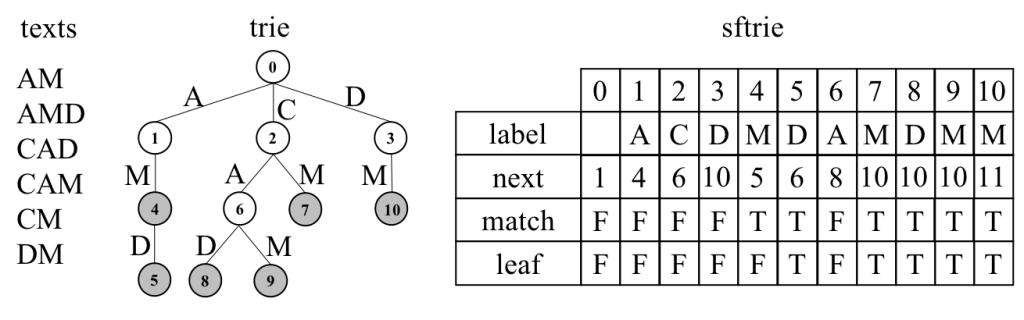
以降はこのアルゴリズム、実装および実験結果について解説します。
準備
文字列とトライ
文字列を構成する文字の集合をアルファベットといいます。 ここでいうアルファベットは英数字{A,B,C,...}や漢字・かな文字の他、大きな整数の集合でも構いません。 文字列の集合が与えられたとき、文字でラベル付けされた辺からなるパスで各文字列を表し、共通する接頭辞(文字列の先頭部分)に対応するパスをまとめると、トライを構成することができます。 文字列の集合とそのトライの例を以下の図に示します。 色のついた6個のノードは文字列集合の各文字列に対応します。

トライを根からたどっていくことで、以下の操作を高速に行うことができます。
- クエリと完全一致する文字列の検索
- 与えられた文字列が集合内に存在するかどうかを返す一般的な処理です
- クエリの接頭辞である文字列の検索 (common-prefix search)
- 形態素解析で辞書から単語分割の候補を列挙する際等に用いられます
- クエリを接頭辞とする文字列の検索 (predictive search)
- キー入力時のオートコンプリート等、クエリの次に続く文字列が知りたいときに用いられる処理です
より多くの環境で手軽に文字列集合からの検索を行うには、正規表現やハッシュ表、平衡二分探索木等を用いることも考えられますが、高速性や省メモリ性が求められる場合や、上に挙げたような完全一致以外の検索を高速に行いたい場合には、文字列の集合に特化した索引構造であるトライに優位性があります。
トライの実装
トライを一般的な木構造として実装すると、各ノードについて、子の集合を表すためのポインタと、自身に接続する辺のラベルを格納する必要があり、元の文字列集合に対して比較的多くの領域を消費します。 また、木構造の簡単な実装としては"left-child, right-sibling"等と呼ばれるふたつのポインタを用いた方法がありますが、アルファベットサイズ|Σ|に対して最適な計算量であるO(log|Σ|)時間を保障するためには平衡二分木等を用いる必要があり、実装が複雑になりがちです。
一方、現実に広く使われているアプローチとしては、配列で表現されたトライの表引きによる高速な検索を提供するダブル配列や、簡潔データ構造を用いて元の文字列データより小さなサイズを実現するもの、ハッシュ表を組み合わせたコンパクトで高速なもの等があります。
しかし最適化された実装では文字型を8ビットの固定サイズに限定しているのが一般的であり、より大きなアルファベットを扱いたい場合、日本語テキストならばUTF-8符号化を用いたり、32ビット整数ならば8ビット毎に分割して扱うなど、入力データ側の工夫が必要となります。
そこで本記事では、固定のアルファベットサイズを仮定せず、かつコンパクトに表現でき高速に検索できるトライの実現について考えます。
データ構造
文字とノードの関係
文字列の集合とトライの関係をより詳細に見るため、各文字列を縦書きで左から順に並べてみます。
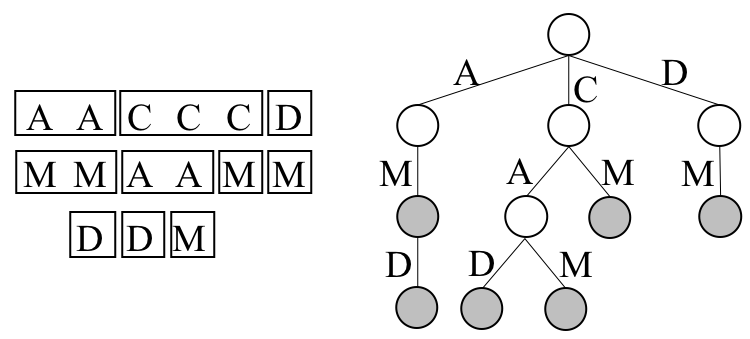
深さ(文字列の先頭から何文字目か)別に見ていくと、文字列集合において左右に同じ文字が続く範囲がひとつのノードとなり、そのノードを根とした部分木は同じ範囲の文字列で構成されていることがわかります。
ノードの順序付け
文字列集合全体を対象として深さ1(1文字目)で走査した後、1文字目で得た範囲毎に深さ2で順に走査すると、トライを幅優先順で探索することができます。 しかしここで、深さ1での全体の走査が終わった後、根のそれぞれの子について、その子を根とする部分木をすべて走査してから、次の子に対応する範囲の走査を行うことにします。 つまり、探索全体としては深さ優先的であるものの、次の深さに進む前にはまず兄弟だけを幅優先的に走査していくという方針です。これを兄弟優先探索と呼びます。 兄弟優先順でトライを走査してノードに番号を振ると下の図のようになります。
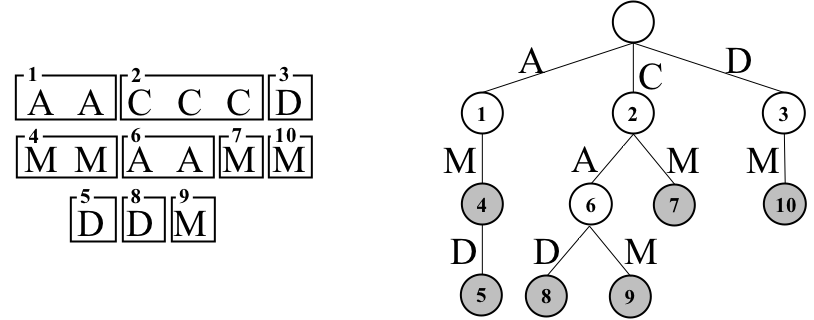
ここでトライのノードuについて、兄弟優先探索におけるuの次のノードを、兄弟優先順でuより後に探索されるノードの中で、uの兄のすべての子孫、およびuの弟を除いて最初に探索されるノードと定義します。 任意の葉でないノードについて、次のノードは最初の子です。 兄弟優先順でトライTのノードを根から探索するとき、任意のノードT[i]について、T[i]の次のノードをT[i].nextで表します。T[i]に次のノードが存在しないとき、T[i].next≡|T|+1と定義します。
兄弟優先探索に基づくトライ表現
文字列の集合Sに対するsftrieとは、Sのトライのノードを兄弟優先順に並べた列Tであり、Tの各ノードT[i] (0≦i≦|T|)は次の四つ組{label, next, leaf, match}で表されます:
- T[i].label: T[i]に向かう辺に割り当てられた文字
- T[i].next: T[i]の次のノードの位置
- T[i].leaf: T[i]が葉かどうかを表すフラグ
- T[i].match: T[i]がS中の文字列を表すかどうかを表すフラグ
例を下の図に示します。 アルファベットサイズを|Σ|、トライの総ノード数を|T|とすると、sftrieは|T|・(log|Σ|+log|T|+2)ビットで表すことができます。 なお、ノードを隙間なく並べた構造から明らかなように、動的な追加や削除は想定していません。

子の探索
兄弟優先探索順でノードを配置すると以下の性質が得られます。
- 任意のノードuのすべての子はu.nextから始まるTの領域にラベル付けされた文字の昇順で連続して現れる
- 葉でない任意のノードuについて、uの子はT[u.next .. T[u.next].next]の範囲に連続して配置される
1つ目の性質は探索順の定義より明らかです。これにより、特定のラベルを持つ子を二分探索で見つけることができます。
2つ目の性質は以下のように示すことができます: まず1つ目の性質より、uのすべての子はT中のある領域T[p..q] (p≦q)に連続して配置され、pについては
p=u.next
が成り立ちます。 さらに、uの最初の子T[p]を根とするTの部分木はT[q]の直後から始まる範囲に配置されるため、T[p]の次のノードの位置T[p].nextは
T[p].next = q + 1
となります。 ここで1つ目の式を代入すると
T[u.next].next = q + 1
移項すれば
q = T[u.next].next - 1
が得られます。 これは、親uに対して子の始点であるnextのみ保持すれば終点qも2回の配列アクセスで求められることを示します。 ただし葉vに対しては一般的にv.next > T[v.next].nextは成り立たないことに注意します。Tがleafフラグを持つのはこのためです。
アルゴリズム
構築および検索の概要を説明します。 なおC++による最小限の実装もありますので、よろしければ合わせてご覧ください。
構築
構築は簡単です。 兄弟優先順となるよう文字列集合を走査すればトライの木構造とラベルが確定できるので、あとは次のノードの位置とふたつのフラグ情報を正しく設定すれば完成です。
以下に擬似コードを示します。
algorithm SFT(S: array of strings)
T = [] # empty array of nodes
T.append({ label: any symbol, next: 1, match: false, leaf: false })
construct(S, 1, |S|, 1, T, 1)
return T
algorithm construct(S, begin, end, depth, T, current)
if(d > |S[s]|)
T[current].match = true
if(++begin == end)
T[current].leaf = true
return
P = [] # empty array of integers
P.append(begin)
for(i = begin; i < end; )
T.append({ label: S[i][depth], next: NaN, match: false, leaf: false })
while(i < end && S[i][depth] == S[i+1][depth])
++i
P.append(i)
for(k = 1; k < |P| - 1; k = k + 1)
T[T[i].next + k].next = |T| + 1
construct(S, k, k + 1, depth + 1, T, T[current].next + k)
ステップ毎の構築の様子を以下の図に示します。
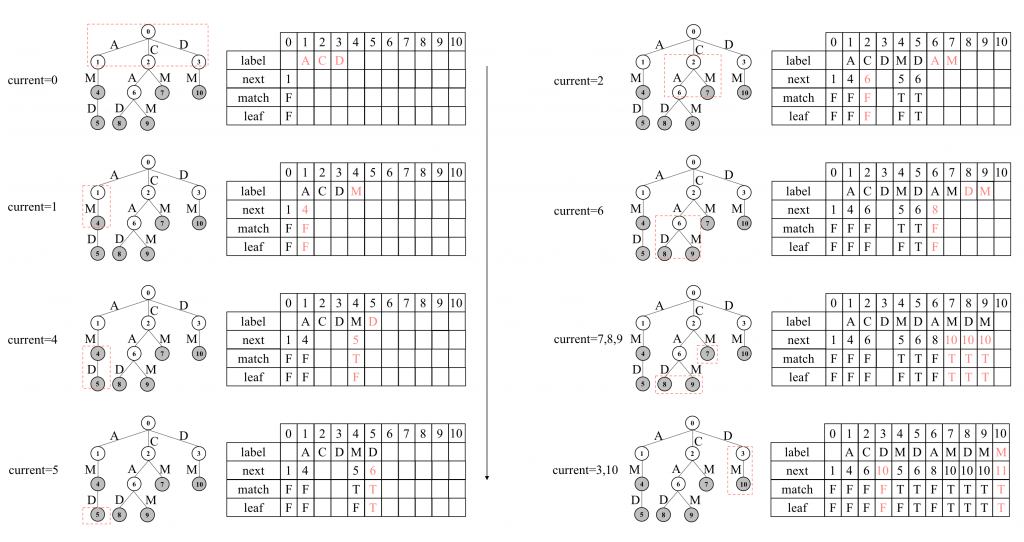
簡単のため、位置0にトライの根を配置します。labelは使わないため任意の文字で問題ありません。next=1です。以降、深さ=1、つまりS中の全文字列の1文字目を対象に文字列集合を走査し、根のそれぞれの子に対して再帰的にトライの構築を進めます。
再帰呼び出しの各段階では、Sの部分集合S[begin..end]のd番目の文字S[begin][depth]..S[end][depth]を走査します。 得られたユニークな文字について、T[current]の子T[p..q]をそれぞれ配置した上、それらの子を根として再帰呼び出しを繰り返します。
ここで、すべての子T[p..q]をnextが未確定のまま先に配置してから、それぞれの子T[k] (p≦k≦q)を根とした再帰呼び出しを実行します。 これによりTのすべてのノードは兄弟優先順で配置されます。
また、再帰呼出しの直前にはT[k].nextにその時点での|T|+1を割り当て、それが変わることはありません。 ここでT[k]に子が存在すれば、最初の子を配置する位置は直前までに構築したTの末尾となり、T[k].nextを正しく与えらることは明らかです。
T[k]が葉のときは、同様にその時点の|T|+1が割り当てられた後、T[k]の子の配置やそれらへの再帰呼び出しも行われません。 つまり|T|が不変のまま再帰呼び出しが終了します。 ここで、兄弟優先順でT[k]より後に探索されるノードを考えると、T[k]のすべての兄に対しては既に再帰呼び出しが行われ、それらの子孫はTに配置されており、またT[k]の弟もnextが未確定のままT上に配置されています。 したがって、T[k]の後で兄弟優先順に実行される再帰呼び出しの中で初めて新たなノードが配置されたとき、T[k].nextはそのノード、すなわちT[k]の次のノードの位置を正しく指すことができます。 最後に、葉T[k]を配置した後一度も他のノードが配置されず構築が完了した場合も、T[k].nextが最終的な|T|+1となるため、結局T[k].nextは正しい値であることがわかります。
各呼び出しにおいて作られる子の数は走査する文字数を上回ることはありません。 また、再帰呼び出しの合計回数は最終的に作られるノードの数と等しいため、Sの総文字数でおさえられます。 さらに、すべての再帰呼び出しをならして考えると、S中の各文字はそれぞれちょうど一度だけ走査さるため、sftrieはSの総文字数に比例する時間で構築することができます。
検索
検索は各深さ毎の二分探索によって実現します。 以下に完全一致検索の擬似コードを示します。
algorithm search(T, pattern)
u = 0
for(i = 1; i < |pattern|; i++)
if(T[u].leaf)
return false
u = T[u].next
v = T[u].next - 1
while(u < v)
m = (u + v) / 2
if(T[m].label < pattern[i])
u = m + 1
else
v = m
if(u > v || T[u].label != pattern[i])
return false
return T[u].match
トライの根から探索を始め、パターンの各文字毎に二分探索で子のラベルを確認していきます。最後にたどり着いたノードのmatchが真ならば完全一致する文字列が存在します。 各深さで子の数は最大|Σ|個なので、検索の計算量はO(|s|log|Σ|)時間です。
Common-prefix searchは、各文字毎にたどったノードのmatchを調べ、真ならば根から現在のノードまでの文字列を報告していけば同じ計算量で実現できます。
Predictive searchは、完全一致を行った後、たどり着いたノードを根として、自身を含むすべての子孫を探索してmatchが真であるノードを列挙すれば実現できます。 sの完全一致検索に要する時間に加え、部分木のノード数に比例する時間がかかります。 また、パターン長分の位置情報のスタックが追加領域として必要ですが、各深さ毎に現在たどっている子を覚えておけば、深さ優先探索により辞書順で検索結果を列挙することができます。
実装
実装上の改善
実際の文字列集合は一般にすべての可能な文字列に対して偏ったものであり、その性質を利用して効率化を図ることができます。 今回はtail圧縮と子ノード展開というふたつの簡単な手法を導入しました。
tail圧縮
実際のデータでトライを構築すると、葉までのパスが一本道になるような構造が多く見られます。 この各ノードをそれぞれ四つ組で表す代わりに一組の文字列とポインタで表すことで、索引構造全体のサイズ削減を試みます。 これをtail圧縮と呼びます。
今回行った実装では、このような文字列を格納する共通の配列と、個別の文字列の開始位置を指す各ノードの開始位置により実装しました。 tail圧縮が行われないノードも開始位置を格納する必要がある代わりに、次のノードの開始位置から終了位置を求めることができるため、各ノードの追加領域は整数ひとつ分です。
子ノード展開
実際のデータでトライを構築すると、特定のノードが非常に多くの子を持ち、他の多数のノードは少ない数の子しか持たないような傾向が見られます。 このように多くの子を持つノードに対しては、実際には存在しないノードも含めてすべての文字でラベル付けされた子を配列上に確保し、検索時に1回の表引きでアクセスできるようにします。 ただし、展開を行うノードそれぞれについてアルファベットサイズに比例した時間と領域がかかるため、トライ全体に対して十分少ない割合で行うよう注意する必要があります。
インターフェース
setとmap
setは文字列集合のみを格納し、mapは各文字列とそれらに紐付けられた値を格納します。
テンプレートパラメーター
次の型を指定できます:
- 文字
- char, char16_t, long long int等の整数型
- 文字列に紐付けられた値
- mapのみ
- 位置
- 通常は32ビット。必要な場合は索引サイズに合わせて指定
利用
サンプルプログラム
文字列の集合からトライを構築し、検索を行うプログラムの簡単なサンプルです。
実行すると、第一引数に指定したファイルの各行を文字列として読み込み、行数を値として紐づけたmapを構築します。 その後は標準入力から与えられたパターンを検索し、存在すれば行数を表示します。 パターンの最後に"?"を付けるとcommon-prefix searchを、"*"を付けるとpredictive searchを行います。
ヘッダファイル
ヘッダファイルのみから構成されているため、パスの通ったディレクトリに
sftrie/*.hpp
を配置し、以下のように読み込んでください。
#include <sftrie/set.hpp>
#include <sftrie/map.hpp>構築
以下のようにしてトライを構築できます:
std::vector<std::string> texts = {"abc", "def", "ghi"};
sftrie::set<std::string> index(std::begin(texts), std::end(texts));検索
完全一致検索は次のように行います:
std::string pattern = "abc";
if(index.exists(pattern))
std::cout << pattern << " exists" << std::endl;Common-prefix searchを行い、得られた文字列を表示するには以下のように書きます:
auto searcher = index.searcher();
for(const auto& result: searcher.prefix(pattern))
std::cout << result << std::endl;Predictive searchを行い、得られた文字列を表示するには以下のように書きます:
for(const auto& result: searcher.traverse(pattern))
std::cout << result << std::endl;実験
データ
Wikipediaの英語版および日本語版の全エントリー名のリストを用いました。
それぞれのデータの概要を下の表にまとめました。 日本語版についてはUTF-16符号化を用いた実験も行ったため、そちらの情報も併記しています。
| Wikipedia英語版 | Wikipedia日本語版 (UTF-8) | Wikipedia日本語版 (UTF-16) | |
|---|---|---|---|
| エントリー数 | 14,277,793 | 1,821,928 | 1,821,928 |
| 総文字数 | 289,030,515 | 39,389,018 | 14,885,900 |
| アルファベットサイズ | 199 | 189 | 9,134 |
| 平均文字数 | 20.2 | 21.62 | 8.17 |
これらのデータに対してトライを構築し、同じデータ中の全文字列をランダムに並べ替えたものをクエリとしてそれぞれ完全一致検索を行いました。
手法
以下の実装を比較しました。 なお参考として、よく知られた既存のトライ実装であるDarts cloneとlibmarisaについても同じ環境・データで実験しています。
- sftrie::set/original: オリジナルのsftrieによるset
- ただし子の数が40未満のとき二分探索から線形探索に切り替え
- sftrie::set/tail: original + tail圧縮
- sftrie::set/decomp: tail + 子ノード展開
- UTF-8のとき: 子の数が48以上で展開
- UTF-16のとき: 子の数が800以上で展開
- sftrie::map/original: sftrie::set/originalに値として32ビット整数を紐づけたmap
- sftrie::map/tail: sftrie::set/tailのmap版
- sftrie::map/decomp: sftrie::set/decompのmap版
- Darts clone/val=0: Darts cloneですべての文字列に値として0を紐づけたもの
- Darts clone/val=n: Darts cloneですべての文字列に一意な整数値を紐づけたもの
- libmarisa/t=1: libmarisaでトライの数を1としたもの
- libmarisa/t=5: libmarisaでトライの数を5としたもの
線形探索や子ノード展開を行うパラメーターは予備実験により求めた値を用いました。
結果
検証環境はUbuntu 18.04、Intel Core i5-6500、g++ 7.3.0です。
Wikipedia英語版
| 索引サイズ[MB] | 構築時間[ナノ秒/クエリ] | 検索時間[ナノ秒/クエリ] | |
|---|---|---|---|
| sftrie::set/original | 625.06 | 419.4 | 750.4 |
| sftrie::set/tail | 384.93 | 171.7 | 728.7 |
| sftrie::set/decomp | 389.03 | 185.6 | 649.6 |
| sftrie::map/original | 1125.11 | 460.1 | 836.8 |
| sftrie::map/tail | 514.90 | 195.6 | 784.6 |
| sftrie::map/decomp | 520.82 | 199.5 | 691.8 |
| Darts clone/val=0 | 195.28 | 1567.0 | 552.6 |
| Darts clone/val=n | 557.65 | 3984.0 | 553.8 |
| libmarisa/t=1 | 101.57 | 1262.5 | 1666.0 |
| libmarisa/t=5 | 73.31 | 1422.6 | 2377.5 |
originalとtail/decompを比べると、tail圧縮の導入で索引サイズと構築時間が、子ノード展開により検索時間が改善していることがわかります。 setとmapの比較では、originalでは1ノードのサイズが6バイトから10バイトに増えるため、索引全体のサイズにそのまま影響していますが、tail圧縮を行うと、tail文字列を格納する領域の他に1ノードあたり4バイト増加する一方、ノード数は大幅に抑えられるため、サイズの増加は3割ほどとなります。 sftrie::set/decompをDarts clone/val=0と比べると、構築時間が短いことを除けば、索引サイズが約2倍、検索時間は17%程度余計にかかっています。 sftrie::map/decompとDarts clone/val=nでは、索引サイズは若干コンパクトであるものの、検索時間はsftrieのみsetよりやや遅くなり差が25%程度に開いています。 libmarisaはデータ構造の特性上検索時間がややかかるものの他より明確にコンパクトな索引サイズを実現しています。
Wikipedia日本語版
sftrieについてはUTF-16での結果も載せています。
| 索引サイズ[MB] | 構築時間[ナノ秒/クエリ] | 検索時間[ナノ秒/クエリ] | |
|---|---|---|---|
| sftrie::set/original | 91.27 | 493.2 | 621.3 |
| sftrie::set/tail | 52.10 | 179.0 | 500.0 |
| sftrie::set/decomp | 52.33 | 191.4 | 465.6 |
| sftrie::map/original | 164.29 | 550.3 | 569.8 |
| sftrie::map/tail | 69.02 | 204.8 | 524.2 |
| sftrie::map/decomp | 69.35 | 208.1 | 494.4 |
| sftrie::set/original (UTF-16) | 45.15 | 194.0 | 396.0 |
| sftrie::set/tail (UTF-16) | 36.28 | 99.3 | 411.2 |
| sftrie::set/decomp (UTF-16) | 39.45 | 113.1 | 353.9 |
| sftrie::map/original (UTF-16) | 75.25 | 215.7 | 420.3 |
| sftrie::map/tail (UTF-16) | 46.89 | 116.9 | 437.4 |
| sftrie::map/decomp (UTF-16) | 51.33 | 120.7 | 376.1 |
| Darts clone/val=0 | 30.94 | 1580.0 | 415.9 |
| Darts clone/val=n | 80.45 | 3665.0 | 413.3 |
| libmarisa/t=1 | 15.64 | 1089.0 | 948.50 |
| libmarisa/t=5 | 10.14 | 1275.9 | 1489.1 |
UTF-8を用いたときの結果は概ねWikipedia英語版と同じ傾向ですが、UTF-16で文字列を扱うことでsftrieのすべての項目が改善したことがわかります。 sftrie::set/decompを見ると、索引サイズは(UTF-8で符号化された)元のテキストと同程度となり、構築時間は約41%、検索時間は約24%改善しました。 また、構築時間を除くと、最も単純なoriginalと最適化を図ったtail/decompの差が縮小していることも興味深い結果といえます。
おわりに
この記事では簡単なトライとその実装sftrieを紹介しました。
明日はfreddiewangさんの"The power of Kotlin’s DSL and script engine"です。お楽しみに。
